题目内容
1.实数x,y满足的不等式组$\left\{\begin{array}{l}{x≥1}\\{y≥1}\\{x+y≤3}\end{array}\right.$所表示的平面区域面积为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
分析 由约束条件作出可行域,联立方程组求出三角形三个顶点的坐标,进一步得到两直角边的长度,代入三角形面积公式得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x≥1}\\{y≥1}\\{x+y≤3}\end{array}\right.$作出可行域如图,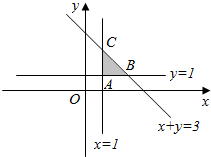
A(1,1),
联立$\left\{\begin{array}{l}{y=1}\\{x+y=3}\end{array}\right.$,得B(2,1),
联立$\left\{\begin{array}{l}{x=1}\\{x+y=3}\end{array}\right.$,得C(1,2),
∴|AB|=1,|AC|=1,
则${S}_{△ABC}=\frac{1}{2}×1×1=\frac{1}{2}$.
故选:A.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是基础题.

练习册系列答案
相关题目
9.函数f(x)=x2-x-2,x∈[-5,5],在定义域内任取一点x0,使f(x0)>0的概率是( )
| A. | $\frac{3}{10}$ | B. | $\frac{2}{3}$ | C. | $\frac{7}{10}$ | D. | $\frac{4}{5}$ |
16.已知函数y=x2-6x+8在[1,a]为减函数,则a的取值范围是( )
| A. | a≤3 | B. | 1<a≤3 | C. | a≥3 | D. | 0≤a≤3 |
6.在100$\sqrt{3}$m高的山顶上,测得山下一塔顶与塔底的俯角分别是30°、60°,则塔高为( )
| A. | $\frac{400}{3}$m | B. | $\frac{400\sqrt{3}}{3}$m | C. | $\frac{200\sqrt{3}}{3}$m | D. | $\frac{200}{3}$m |
 如图,直线PA与圆相切于点A,过P作直线与圆交于C、D两点,点B在圆上,且∠PAC=∠BCD.
如图,直线PA与圆相切于点A,过P作直线与圆交于C、D两点,点B在圆上,且∠PAC=∠BCD.