Question

设某几何体及其三视图：如图（尺寸的长度单位：m）
（1）O为AC的中点，证明：BO⊥平面APC；
（2）求该几何体的体积；
（3）求点A到面PBC的距离．

Answer 1

分析：（1）面PAC⊥面ABC，BO⊥AC，由两个平面垂直的性质可得BO⊥平面APC．
（2）过P点在面PAC内作PE⊥AC交AC于E，则PE是锥体的高，等于2，求出S_△ABC ，代入锥体的体积公式进行运算．
（3）余弦定理求的cos∠PBC，利用同角三角函数的基本关系求得sin∠PBC，求出S_△PBC，利用V_A-PBC=V_P-ABC=

1

3

h•S_△PBC=4，求出点A到面PBC的距离h 的值．

解答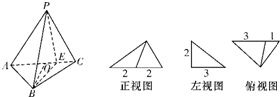：解：（1）证明：由三视图可知，面PAC⊥面ABC，BO⊥AC，
∴BO⊥平面APC．
（2）过P点在面PAC内作PE⊥AC交AC于E，
由俯视图可知：CE=1，AE=3
又BO=3，AC=4，∴S_△ABC=

1

2

×4×3=6，
∴V_P-ABC=

1

3

×6×2=4．
（3）∵PC=

PE2+EC2

=

5

，BE=

BO2+OE2

=

10

，∴PB=

BE2+PE2

=

14

，
BC=

BO2+OC2

=

13

，∴cos∠PBC=

PB2+BC2-PC2

2PB•BC

=

14+13-5

2 14 • 13

=

22

2 14×13

=

11

14×13

．
∴sin∠PBC=

1- 121 14×13

=

61 14×13

，∴S_△PBC=

1

2

PB•BC•sin∠PBC=

1

2

14

•

13

•

61

14•13

=

61

2

．
设点A到面PBC的距离为h．∵V_A-PBC=V_P-ABC=

1

3

h•S_△PBC=4，
∴h=

12

S△_PBC

=

12

61 2

=

24 61

61

．

点评：本题考查证明线面垂直的方法，求棱锥的体积，体现了数形结合的思想，求三角形PBC的面积是解题的难点．