题目内容
如图,在多面体ABCDEF中,底面ABCD是梯形,且AD=DC=CB= AB.直角梯形ACEF中,
AB.直角梯形ACEF中, ,
, 是锐角,且平面ACEF⊥平面ABCD.
是锐角,且平面ACEF⊥平面ABCD.
(1)求证: ;
;
(2)若直线DE与平面ACEF所成的角的正切值是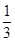 ,试求
,试求 的余弦值.
的余弦值.
(1)详见试题解析;(2)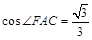 .
.
解析试题分析:(1)证明线线垂直,可转化为证明线面垂直.要证 ,只要证
,只要证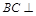 平面
平面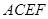 ,由已知平面ACEF⊥平面ABCD,故由面面垂直的性质定理知,只要证
,由已知平面ACEF⊥平面ABCD,故由面面垂直的性质定理知,只要证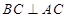 .在等腰梯形ABCD中,由已知条件及平面几何相关知识易得
.在等腰梯形ABCD中,由已知条件及平面几何相关知识易得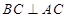 ;(2)连结
;(2)连结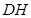 交
交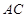 于
于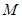 ,再连结EM,FM,易知四边形
,再连结EM,FM,易知四边形 为菱形,∴DM⊥AC,注意到平面
为菱形,∴DM⊥AC,注意到平面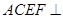 平面
平面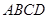 ,故DM⊥平面
,故DM⊥平面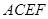 .于是,
.于是,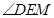 即为直线DE与平面ACEF所成的角.在
即为直线DE与平面ACEF所成的角.在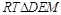 中由锐角三角函数可求得
中由锐角三角函数可求得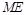 的长,再在
的长,再在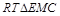 中由锐角三角函数即可求得
中由锐角三角函数即可求得 的余弦值.
的余弦值.
试题解析:(1)证明:在等腰梯形ABCD中,∵AD=DC=CB= AB,∴AD、BC为腰,取AB得中点H,连CH,易知,四边形ADCH为菱形,则CH=AH=BH,故△ACB为直角三角形,
AB,∴AD、BC为腰,取AB得中点H,连CH,易知,四边形ADCH为菱形,则CH=AH=BH,故△ACB为直角三角形,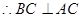 . 3分
. 3分 平面
平面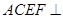 平面
平面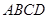 ,且平面
,且平面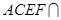 平面
平面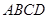
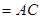 ,
,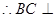 平面
平面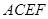 ,而
,而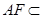 平面
平面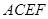 ,故
,故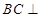
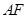 . 6分
. 6分
(2)连结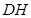 交
交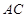 于
于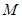 ,再连结EM,FM,易知四边形
,再连结EM,FM,易知四边形 为菱形,∴DM⊥AC,注意到平面
为菱形,∴DM⊥AC,注意到平面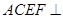 平面
平面 ,故DM⊥平面
,故DM⊥平面 .于是,
.于是,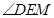 即为直线DE与平面ACEF所成的角. 9分
即为直线DE与平面ACEF所成的角. 9分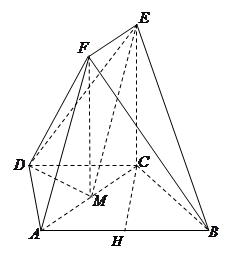
设AD=DC=BC=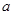 ,则MD=
,则MD=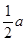 ,
,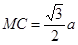 .依题意,
.依题意,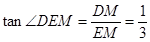 ,
,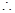
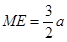 ,在
,在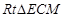 中,
中,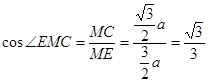 ,∵
,∵ =AM,
=AM,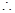 四边形AMEF为平行四边形,
四边形AMEF为平行四边形,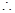
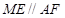 ,
,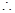
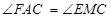 ,
,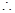
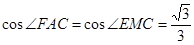 . 12分
. 12分
考点:1.空间垂直关系的证明;2.空间角的计算.

练习册系列答案
相关题目
 EF=2
EF=2 ,AF=BE=2,P、Q、M分别为AE、BD、EF的中点.
,AF=BE=2,P、Q、M分别为AE、BD、EF的中点.



 的值.
的值.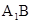 的中点,F是棱CC1上的点.
的中点,F是棱CC1上的点.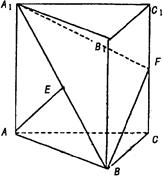
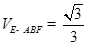 时,求正方形AA1C1C的边长;
时,求正方形AA1C1C的边长;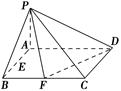
 底面
底面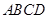 ,且△PAD为等腰直角三角形,
,且△PAD为等腰直角三角形, ,E、F分别为PC、BD的中点.
,E、F分别为PC、BD的中点.
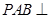 平面
平面 .
.