题目内容
已知y=f(x)是函数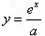
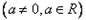 的反函数,
的反函数,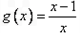
(Ⅰ)解关于x的不等式: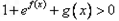 ;
;
(Ⅱ)当a=1时,过点(-1,1)是否存在函数y=f(x)图象的切线?若存在,有多少条?若不存在,说明理由;
(Ⅲ)若a是使f(x)≥g(x)(x≥1)恒成立的最小值,试比较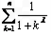 与
与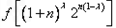 的大小(0<λ<1,n∈N*)
的大小(0<λ<1,n∈N*)
(1)由已知可得f(x)=lnax,
当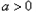 时,f(x)的定义域为
时,f(x)的定义域为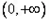 ;
;
当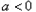 时,f(x)的定义域为
时,f(x)的定义域为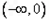
①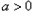 时,
时,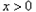 ,原不等式等价于:
,原不等式等价于: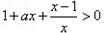
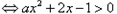 ,
,
可得 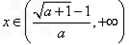 ;
;
②当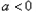 时,
时,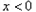 ,原不等式等价于:
,原不等式等价于: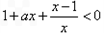
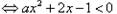 ,
,
可得 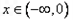 .
.
(2)设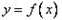 图象上的切点坐标为
图象上的切点坐标为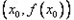 ,显然
,显然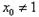 ,
,
可得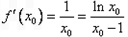
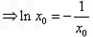 ,
,
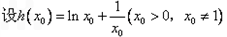 ,
,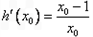
可得h(x0)在(1,+∞)为增区间;(0,1)为减区间,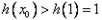
所以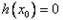 没有实根,故不存在切线.
没有实根,故不存在切线.
(3)∵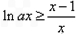 对x≥1恒成立,所以
对x≥1恒成立,所以
∵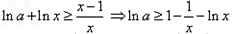 ,
,
令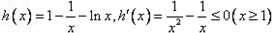 ,
,
可得h(x)在区间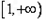 上单调递减,
上单调递减,
故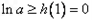 ,
,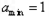 .得
.得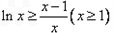 ,f(x)=lnx.
,f(x)=lnx.
令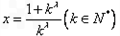 ,
,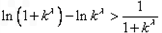 ,
,
而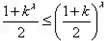 ,即
,即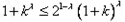 ,
,
所以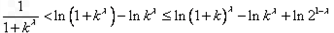 ,
, 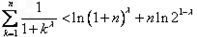 =
=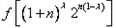 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
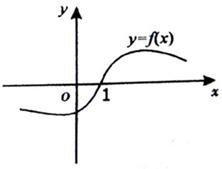 已知函数f(x)(x∈R)的一段图象如图所示,f′(x)是函f(x)(数的导函数,且y=f(x+1)是奇函数,给出以下结论:
已知函数f(x)(x∈R)的一段图象如图所示,f′(x)是函f(x)(数的导函数,且y=f(x+1)是奇函数,给出以下结论: 已知函数f(x)=
已知函数f(x)=