题目内容
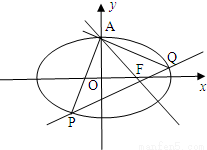
已知椭圆c: +y2=1=1的两焦点为F1,F2,点P(x0,y0)满足0<
+y2=1=1的两焦点为F1,F2,点P(x0,y0)满足0<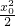 +y02<1,则|PF1|+|PF2|的取值范围为________.
+y02<1,则|PF1|+|PF2|的取值范围为________.
[2,2 )
)
分析:先根据椭圆的定义得到|PF1|+|PF2|=2a,然后根据点P(x0,y0)满足0<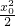 +y02<1,得出点P在椭圆内部,最后根据点P在椭圆上时|PF1|+|PF2|最大,可确定答案.
+y02<1,得出点P在椭圆内部,最后根据点P在椭圆上时|PF1|+|PF2|最大,可确定答案.
解答:由题意可知|PF1|+|PF2|=2a
点P(x0,y0)满足0<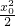 +y02<1,
+y02<1,
得出点P在椭圆内部,且与原点不重合,
∵当点P在椭圆上时|PF1|+|PF2|最大,
最大值为2a=2 ,而点P在椭圆内部,
,而点P在椭圆内部,
∴|PF1|+|PF2|<2
∵当点P在线段F1F2上除原点时,|PF1|+|PF2|最小,最小值为2,
∴|PF1|+|PF2|>2
则PF1+PF2的取值范围为[2,2 )
)
故答案为[2,2 ).
).
点评:本题主要考查椭圆的定义、椭圆的简单性质,解答的关键是在区域的边界上利用椭圆的定义,即椭圆上点到两焦点的距离的和等于2a.定义法是解决此类的常用方法.
 )
)分析:先根据椭圆的定义得到|PF1|+|PF2|=2a,然后根据点P(x0,y0)满足0<
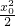 +y02<1,得出点P在椭圆内部,最后根据点P在椭圆上时|PF1|+|PF2|最大,可确定答案.
+y02<1,得出点P在椭圆内部,最后根据点P在椭圆上时|PF1|+|PF2|最大,可确定答案.解答:由题意可知|PF1|+|PF2|=2a
点P(x0,y0)满足0<
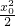 +y02<1,
+y02<1,得出点P在椭圆内部,且与原点不重合,
∵当点P在椭圆上时|PF1|+|PF2|最大,
最大值为2a=2
 ,而点P在椭圆内部,
,而点P在椭圆内部,∴|PF1|+|PF2|<2

∵当点P在线段F1F2上除原点时,|PF1|+|PF2|最小,最小值为2,
∴|PF1|+|PF2|>2
则PF1+PF2的取值范围为[2,2
 )
)故答案为[2,2
 ).
).点评:本题主要考查椭圆的定义、椭圆的简单性质,解答的关键是在区域的边界上利用椭圆的定义,即椭圆上点到两焦点的距离的和等于2a.定义法是解决此类的常用方法.

练习册系列答案
相关题目
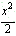 + y2=1的右焦点为F,右准线为l,点A∈l,线段AF交C于点B,若
+ y2=1的右焦点为F,右准线为l,点A∈l,线段AF交C于点B,若 = 3
= 3 ,则|
,则| |等于
|等于
 B、2 C、
B、2 C、 D、3
D、3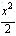 + y2=1的右焦点为F,右准线为l,点A∈l,线段AF交C于点B,若
+ y2=1的右焦点为F,右准线为l,点A∈l,线段AF交C于点B,若 = 3
= 3 ,则|
,则| |等于
|等于
 B、2 C、
B、2 C、 D、3
D、3 +y2=1及定点A(2,0),点P是椭圆上的动点,则|PA|的最小值为( )
+y2=1及定点A(2,0),点P是椭圆上的动点,则|PA|的最小值为( )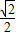


 +y2=1(a>1)的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0相切.
+y2=1(a>1)的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0相切.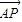 •
• =0.求证:直线l过定点,并求出该定点的坐标.
=0.求证:直线l过定点,并求出该定点的坐标.
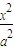 +y2=1(a>1)的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0相切.
+y2=1(a>1)的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0相切.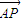 •
•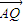 =0.求证:直线l过定点,并求出该定点的坐标.
=0.求证:直线l过定点,并求出该定点的坐标.