题目内容
一般地,如果函数f(x)的图象关于点(a,b)对称,那么对定义域内的任意x,则f(x)+f(2a-x)=2b恒成立.已知函数f(x)=
的图象关于点M(
,
)对称,则常数m的值为 .
| 4x |
| 4x+m |
| 1 |
| 2 |
| 1 |
| 2 |
考点:函数奇偶性的性质,函数的图象与图象变化
专题:函数的性质及应用
分析:根据函数关于点对称的关系式,解方程即可得到结论.
解答:
解;∵函数f(x)=
的图象关于点M(
,
)对称,
∴f(x)+f(1-x)=1,
即当x=
时,f(
)+f(
)=1,
即f(
)=
,
则f(
)
=
=
,解得m=2,
故答案为:2
| 4x |
| 4x+m |
| 1 |
| 2 |
| 1 |
| 2 |
∴f(x)+f(1-x)=1,
即当x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即f(
| 1 |
| 2 |
| 1 |
| 2 |
则f(
| 1 |
| 2 |
4
| ||
4
|
| 2 |
| 2+m |
| 1 |
| 2 |
故答案为:2
点评:本题主要考查函数对称性的应用,根据定义建立方程是解决本题的关键.

练习册系列答案
相关题目
已知y=f(x)是偶函数,且在区间(0,+∞)上是增函数,则f(-4)、f(π)、f(-1)的大小关系是( )
| A、f(π)>f(-1)>f(-4) |
| B、f(-1)>f(-4)>f(π) |
| C、f(-4)>f(π)>f(-1) |
| D、f(-4)>f(-1)>f(π) |
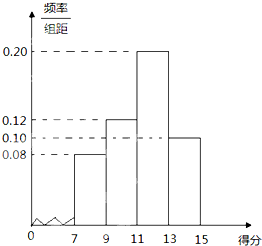 某中学高三年级共有学生1000人参加期中考试,今随机抽取50人,对本次考试数学卷第20题的得分情况进行统计,其频率分布直方图如图,在本年级中估计该题得分不低于11分的学生人数有
某中学高三年级共有学生1000人参加期中考试,今随机抽取50人,对本次考试数学卷第20题的得分情况进行统计,其频率分布直方图如图,在本年级中估计该题得分不低于11分的学生人数有