题目内容
已知函数f(x)=ax-bxln x,其图象经过点(1,1),且在点(e,f(e))处的切线斜率为3.(e为自然对数的底数).
(1)求实数a、b的值;
(2)若k∈Z,且k<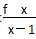 对任意x>1恒成立,求k的最大值;
对任意x>1恒成立,求k的最大值;
(3)证明:2ln 2+3ln 3+…+nln n>(n-1)2(n∈N*,n>1).
【解】 (1)因为f(1)=1,所以a=1,
此时f(x)=x-bxln x,f′(x)=1-b(1+ln x),
依题意,f′(e)=1-b(1+ln e)=3,所以b=-1.
(2)由(1)知:f(x)=x+xln x,
当x>1时,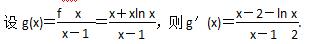
设h(x)=x-2-ln x,则h′(x)=1-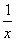 >0,h(x)在(1,+∞)上是增函数.
>0,h(x)在(1,+∞)上是增函数.
因为h(3)=1-ln 3<0,h(4)=2-ln 4>0,
所以,存在x0∈(3,4),使h(x0)=0.
当x∈(1,x0)时,h(x)<0,g′(x)<0,即g(x)在(1,x0)上为减函数;
同理g(x)在(x0,+∞)上为增函数,从而g(x)的最小值为g(x0)=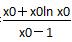 ,
,
所以x0∈(3,4),k的最大值为3.
(3)证明 由(2)知,当x>1时,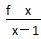 >3,
>3,
所以f(x)>3x-3,即x+xln x>3x-3,xln x>2x-3,
所以2ln 2+3ln 3+…+nln n>(2×2-3)+(2×3-3)+…+(2n-3)=2(2+3+…+n)-3(n-1)=2× -3n+3=n2-2n+1=(n-1)2(n∈N*,n>1).
-3n+3=n2-2n+1=(n-1)2(n∈N*,n>1).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
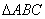 中,内角
中,内角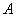 ,
,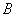 ,
,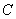 的对边分别为
的对边分别为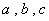 .已知
.已知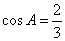 ,
,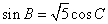
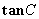 的值;(2)若
的值;(2)若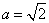 ,求
,求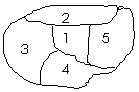
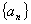 满足
满足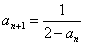 ,
,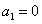 .
.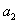 ,
,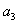 ,
,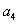 ,
,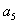 的值;
的值; 与
与 的夹角为
的夹角为 ,
, 则
则 ( )
( ) B
B  C 4 D 12
C 4 D 12 与
与 的夹角是钝角,则k的取值范围是 .
的夹角是钝角,则k的取值范围是 . 上任取一个数
上任取一个数 ,则使得
,则使得 的概率为( )
的概率为( ) B.
B. C.
C. D.
D.
 中,若
中,若 ,则
,则 ()
() D.2
D.2