题目内容
(本大题满分13分)如图,现有一块半径为2m,圆心角为 的扇形铁皮
的扇形铁皮 ,欲从其中裁剪出一块内接五边形
,欲从其中裁剪出一块内接五边形 ,使点
,使点 在
在 弧上,点
弧上,点 分别在半径
分别在半径 和
和 上,四边形
上,四边形 是矩形,点
是矩形,点 在弧
在弧 上,
上, 点在线段
点在线段 上,四边形
上,四边形 是直角梯形.现有如下裁剪方案:先使矩形
是直角梯形.现有如下裁剪方案:先使矩形 的面积达到最大,在此前提下,再使直角梯形
的面积达到最大,在此前提下,再使直角梯形 的面积也达到最大.
的面积也达到最大.
(Ⅰ)设 ,当矩形
,当矩形 的面积最大时,求
的面积最大时,求 的值;
的值;
(Ⅱ)求按这种裁剪方法的原材料利用率.

【答案】
解:(Ⅰ)先求矩形 面积的最大值:
面积的最大值:
设
 ,
, ,则
,则 ,
,
 ,∴当
,∴当 ,即
,即 时,
时,
此时, ,
, ……………………6分
……………………6分
(Ⅱ)过Q点作 垂足为S,设
垂足为S,设
在 中,有
中,有 ,
,
则 ,
,
∴
 ……… 8分
……… 8分
令 ,∵
,∵ ,∴
,∴ ,
,
此时 ,则
,则 ,
,
当 时,
时, 的最大值为
的最大值为 ………………………… 10分
………………………… 10分
∴方案裁剪出内接五边形 面积最大值为
面积最大值为
 ,即利用率=
,即利用率= ……12分
……12分
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
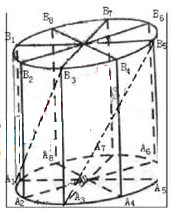 (1)当圆柱底面半径
(1)当圆柱底面半径 ,设
,设 ,数列
,数列 .
.  是等差数列;
是等差数列; 的前n项和Sn;
的前n项和Sn; 一切正整数n恒成立,求实数m的取值范围.
一切正整数n恒成立,求实数m的取值范围. 是椭圆
是椭圆 右焦点,点
右焦点,点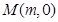 、
、 分别是x轴、 y上的动点,且满足
分别是x轴、 y上的动点,且满足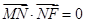 ,若点
,若点 满足
满足 .
. 的方程;
的方程; 、
、 两点,直线
两点,直线 、
、 与直线
与直线 分别交于点
分别交于点 、
、 (其中
(其中 为坐标原点),试判断
为坐标原点),试判断 是否为定值?若是,求出这个定值;若不是,请说明理由.
是否为定值?若是,求出这个定值;若不是,请说明理由. 是定义域在
是定义域在 上的单调函数,且对于任意正数
上的单调函数,且对于任意正数 有
有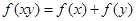 ,已知
,已知 .
.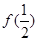 的值;
的值; 满足:
满足: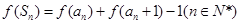 ,其中
,其中 是数列
是数列 ,使
,使

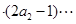
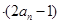 对一切
对一切 成立?若存在,求出M的取值范围;若不存在,说明理由.
成立?若存在,求出M的取值范围;若不存在,说明理由.