题目内容
定义在(0,+∞)上的函数f(x)满足f(x)+f(y)=f(xy),且当x>1时,f(x)<0,若对任意的x,y∈(0,+∞),不等式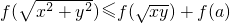 恒成立,则实数a的取值范围是________.
恒成立,则实数a的取值范围是________.

分析:先根据条件证明函数f(x)在(0,+∞)上单调性,然后化简不等式,根据
 ≥
≥ 恒成立建立关系式即可.
恒成立建立关系式即可.解答:设x1>x2>0,则
 >1
>1∵f(x)+f(y)=f(xy),
∴f(x)-f(y)=f(
 ),
),f(x1)-f(x2)=f(
 )<0(x>1时,f(x)<0)
)<0(x>1时,f(x)<0)∴函数f(x)在(0,+∞)上单调递减函数
∵
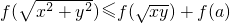
∴f(
 )≤f(a
)≤f(a  )
)即
 ≥a
≥a 
 ≥
≥ ≥a
≥a 
∴a
 ,又a>0.
,又a>0.故答案为:
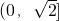
点评:本题主要考查抽象函数的单调性以及不等式的应用,属于中档题,单调性是函数的“局部”性质.

练习册系列答案
相关题目
已知定义在(0,1)上的函数f(x),对任意的m,n∈(1,+∞)且m<n时,都有f(
)-f(
)=f(
)记an=f(
),n∈N*,则在数列{an}中,a1+a2+…a8=( )
| 1 |
| n |
| 1 |
| m |
| m-n |
| 1-mn |
| 1 |
| n2+5n+5 |
A、f(
| ||
B、f(
| ||
C、f(
| ||
D、f(
|