题目内容
已知定义在(0,1)上的函数f(x),对任意的m,n∈(1,+∞)且m<n时,都有f(
)-f(
)=f(
)记an=f(
),n∈N*,则在数列{an}中,a1+a2+…a8=( )
| 1 |
| n |
| 1 |
| m |
| m-n |
| 1-mn |
| 1 |
| n2+5n+5 |
A、f(
| ||
B、f(
| ||
C、f(
| ||
D、f(
|
分析:根据“f(
)-f(
)=f(
)”将“an=f(
)”分拆为“f(
)-f(
)”,再用裂项相消法求“a1+a2+…a8”
| 1 |
| n |
| 1 |
| m |
| m-n |
| 1-mn |
| 1 |
| n2+5n+5 |
| 1 |
| n+2 |
| 1 |
| n+3 |
解答:解:∵f(
)-f(
)=f(
)
∴an=f(
)=f(
)-f(
)
∴a1+a2+…a8=f(
) -f(
) +f(
) -…+f(
) -f(
)
=f(
)-f(
)=f(
)
故选C
| 1 |
| n |
| 1 |
| m |
| m-n |
| 1-mn |
∴an=f(
| 1 |
| n2+5n+5 |
| 1 |
| n+2 |
| 1 |
| n+3 |
∴a1+a2+…a8=f(
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 10 |
| 1 |
| 11 |
=f(
| 1 |
| 3 |
| 1 |
| 11 |
| 1 |
| 4 |
故选C
点评:本题主要考查数列的求和问题,关键是理解数列的规律,即研究透通项,本题的关键是将通项分柝为:an=f(
)=f(
)-f(
).
| 1 |
| n2+5n+5 |
| 1 |
| n+2 |
| 1 |
| n+3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,
已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,下列结论正确的是( )
| A、f(x2)-f(x1)>x2-x1 | ||||
| B、f(x2)-f(x1)<x2-x1 | ||||
C、
| ||||
| D、x2f(x1)>x1f(x2) |
 已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1、x2,给出下列结论:
已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1、x2,给出下列结论: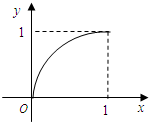 已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论:
已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论: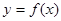 图象如图所示,对于满足0<
图象如图所示,对于满足0<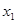 <
<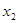 <1的
<1的 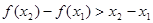 ②
②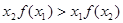 ③
③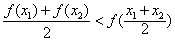 ;
;