题目内容
已知一个四面体其中五条棱的长分别为1,1,1,1,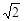 ,则此四面体体积的最大值是
,则此四面体体积的最大值是
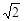 ,则此四面体体积的最大值是
,则此四面体体积的最大值是A.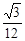 | B.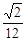 | C.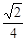 | D.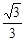 |
A
试题分析:设四面体为P-ABC,则设PC=X,AB=
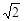 ,其余的各边为1,那么取AB的中点D,那么连接PD,因此可知,AB垂直与平面PCD,则棱锥的体积可以运用以PCD为底面,高为AD,BD的两个三棱锥体积的和来表示,因此只要求解底面积的最大值即可。由于PD=CD=
,其余的各边为1,那么取AB的中点D,那么连接PD,因此可知,AB垂直与平面PCD,则棱锥的体积可以运用以PCD为底面,高为AD,BD的两个三棱锥体积的和来表示,因此只要求解底面积的最大值即可。由于PD=CD= ,那么可知三角形PDC的面积越大,体积越大,因此可知面积的最大值为
,那么可知三角形PDC的面积越大,体积越大,因此可知面积的最大值为 ,也就是当PD垂直于CD时,面积最大,因此可四面体的体积的最大值为
,也就是当PD垂直于CD时,面积最大,因此可四面体的体积的最大值为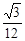 ,选A.
,选A.点评:解决该试题的关键是对于四面体的边长的合理布置,然后进行作相应的辅助线,来借助于垂直的性质,表示多面体的体积,进而得到表达式,结合函数来求解最值,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,则函数
,则函数
 中,
中, ⊥平面
⊥平面 ,
, ⊥平面
⊥平面 ,
, ,
, 为
为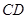 的中点.
的中点.
 ⊥平面
⊥平面 ;
; 的大小.
的大小. 以及平面
以及平面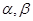 ,下面命题中正确的是
,下面命题中正确的是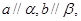 则
则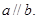
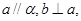 则
则
 则
则
 ,且
,且 ,则
,则
 ,高为
,高为 ,则圆锥的侧面积是
,则圆锥的侧面积是  .
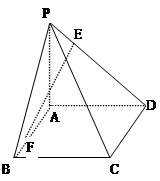
. ,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD
,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD 平面EFDC,设AD中点为P.
平面EFDC,设AD中点为P.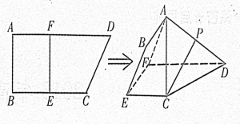
 的棱长为
的棱长为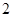 ,长为
,长为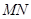 的一个端点
的一个端点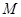 在棱
在棱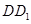 上运动,点
上运动,点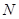 在正方形
在正方形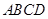 内运动,则
内运动,则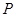 的轨迹的面积为( )
的轨迹的面积为( )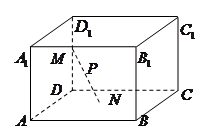
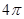
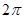
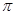
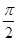
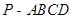 中,底面
中,底面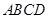 是矩形,
是矩形,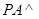 平面
平面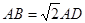 是线段
是线段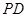 上的点,
上的点,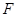 是线段
是线段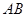 上的点,且
上的点,且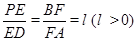
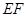 与平面
与平面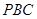 的关系,并证明;
的关系,并证明;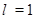 时,证明:面
时,证明:面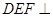 平面
平面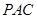 .
.