题目内容
1.已知直线y=kx-1与双曲线x2-y2=4.(1)若直线与双曲线没有公共点,求k的取值范围;
(2)若直线与双曲线只有一个公共点,求k的取值范围.
分析 (1)用代数法,先联立方程,消元后得到一个方程,即判别式小于零,即可求出k的范围
(2)用代数法,先联立方程,消元后得到一个方程,先研究相切的情况,即判别式等于零,再研究与渐近线平行的情况.
解答 解:(1)由题意令$\left\{\begin{array}{l}{{x}^{2}-{y}^{2}=4}\\{y=kx-1}\end{array}\right.$,得x2-(kx-1)2=4,整理得(1-k2)x2+2kx-5=0
当1-k2=0,k=±1时,显然符合条件;
当1-k2≠0时,有△=20-16k2<0,解得k<-$\frac{\sqrt{5}}{2}$或k>$\frac{\sqrt{5}}{2}$.
综上,k取值范围是k=±1,k<-$\frac{\sqrt{5}}{2}$或k>$\frac{\sqrt{5}}{2}$.
(2)由(1)△=0,△=20-16k2=0
∴k=±$\frac{\sqrt{5}}{2}$;
又注意直线恒过点(0,-1)且渐近线的斜率为±1,与渐近线平行时也成立,
∴k=±$\frac{\sqrt{5}}{2}$;k=±1
点评 本题主要考查直线与双曲线的位置关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.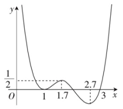 函数f(x)的图象如图所示,则f(x)的极大值点为( )
函数f(x)的图象如图所示,则f(x)的极大值点为( )
 函数f(x)的图象如图所示,则f(x)的极大值点为( )
函数f(x)的图象如图所示,则f(x)的极大值点为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 1.7 | D. | 2.7 |
9.设a=${∫}_{0}^{π}$(sinx+cosx)dx,则二项式($\root{3}{x}$-$\frac{1}{a\sqrt{x}}$)6的展开式中含x2项的系数为( )
| A. | -6 | B. | -1 | C. | 1 | D. | 6 |
16.已知正项等比数列{an}:a9-a8=2a7,若存在两项am,an,使得aman=64a12,则$\frac{1}{m}$+$\frac{9}{n}$的最小值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{5}{2}$ | C. | 16 | D. | 2 |
13.若a>0,且f(x)=x3-ax在[1,+∞)上是增函数,则a的取值范围是( )
| A. | 0<a<3 | B. | 0<a≤3 | C. | a>3 | D. | a≥3 |
10.已知x,y满足线性约束条件:$\left\{\begin{array}{l}{x-y+1≥0}\\{2x+y-2≥0}\\{x-1<0}\end{array}\right.$,则目标函数z=y-3x的取值范围是( )
| A. | $(-1,-\frac{1}{3})$ | B. | (-3,-1) | C. | $(-3,\frac{1}{3}]$ | D. | $[-3,\frac{1}{3}]$ |
11.函数f(x)=ln(2x-x2+3)的定义域为( )
| A. | [-1,3] | B. | (-1,3) | C. | (-∞,-3)∪(1,+∞) | D. | (-∞,-1)∪(3,+∞) |