题目内容
已知条件p:x<1，条件q：
<1，则p是
q的条件 ．
【答案】
既不充分也不必要条件
【解析】
试题分析：根据题意，由于条件p:x<1，条件q：
<1
，那么可知
q：
，因此根据集合之间的互不包含的关系，可知p是q的条件既不充分也不必要条件。
考点：充分条件
点评：判断充要条件的方法是：①若p?q为真命题且q?p为假命题，则命题p是命题q的充分不必要条件；②若p?q为假命题且q?p为真命题，则命题p是命题q的必要不充分条件；③若p?q为真命题且q?p为真命题，则命题p是命题q的充要条件；④若p?q为假命题且q?p为假命题，则命题p是命题q的即不充分也不必要条件．⑤判断命题p与命题q所表示的范围，再根据“谁大谁必要，谁小谁充分”的原则，判断命题p与命题q的关系．
练习册系列答案
相关题目
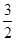）是椭圆E：
（
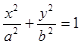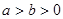）上一点，F1、F2分别是椭圆E的左、右焦点，O是坐标原点，PF1⊥x轴．
（0<λ<4，且λ≠2）．求证：直线AB的斜率等于椭圆E的离心率；