题目内容
过点（0，-4）且与直线y=4相切的圆的圆心轨迹方程是 ．
考点：轨迹方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：先设出动圆圆心的坐标，根据题意可知圆心到定点（0，-4）到直线y=4的距离都等于半径，进而利用抛物线的定义可求得x和y的关系式．
解答：
解：设动圆圆心坐标为（x，y）
∵动圆过定点（0，-4）且与直线y=4相切，
∴圆心到定点（0，-4）到直线y=4的距离都等于半径，
∴根据抛物线的定义可知动圆圆心的轨迹方程是x2=-16y
故答案为：x2=-16y
∵动圆过定点（0，-4）且与直线y=4相切，
∴圆心到定点（0，-4）到直线y=4的距离都等于半径，
∴根据抛物线的定义可知动圆圆心的轨迹方程是x2=-16y
故答案为：x2=-16y
点评：本题考查轨迹方程，利用抛物线的定义来求轨迹方程是关键．
练习册系列答案
相关题目
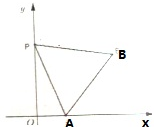如图在平面内放置的边长为1的正三角形PAB沿x轴滚动，设顶点P（x，y）的轨迹方程是y=f（x），则f（x）的最小正周期为