题目内容
等边三角形ABC与正方形ABDE有一公共边AB,二面角C-AB-D的余弦值为 ,M,N分别是AC,BC的中点,则EM,AN所成角的余弦值等于________.
,M,N分别是AC,BC的中点,则EM,AN所成角的余弦值等于________.
 ,M,N分别是AC,BC的中点,则EM,AN所成角的余弦值等于________.
,M,N分别是AC,BC的中点,则EM,AN所成角的余弦值等于________.
设AB=2,作CO⊥平面ABDE,OH⊥AB,则CH⊥AB,∠CHO为二面角C-AB-D的平面角,
CH= ,OH=CH·cos∠CHO=1,结合等边三角形ABC与正方形ABDE可知此四棱锥为正四棱锥,则AN=EM=CH=
,OH=CH·cos∠CHO=1,结合等边三角形ABC与正方形ABDE可知此四棱锥为正四棱锥,则AN=EM=CH= .
.
 =
= (
( +
+ ),
), =
= -
- ,
,
 ·
· =
= (
( +
+ )·
)· =
= .
.
故EM,AN所成角的余弦值为 =
= .
.
CH=
 ,OH=CH·cos∠CHO=1,结合等边三角形ABC与正方形ABDE可知此四棱锥为正四棱锥,则AN=EM=CH=
,OH=CH·cos∠CHO=1,结合等边三角形ABC与正方形ABDE可知此四棱锥为正四棱锥,则AN=EM=CH= .
. =
= (
( +
+ ),
), =
= -
- ,
, ·
· =
= (
( +
+ )·
)· =
= .
.故EM,AN所成角的余弦值为
 =
= .
.
练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
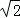 ,点E在侧棱AA1上,点F在侧棱BB1上,且AE=2
,点E在侧棱AA1上,点F在侧棱BB1上,且AE=2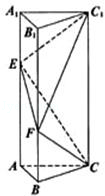
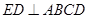 ,ED=1,
,ED=1,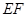 //BD,且
//BD,且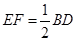 .
.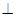 平面BDEF;
平面BDEF;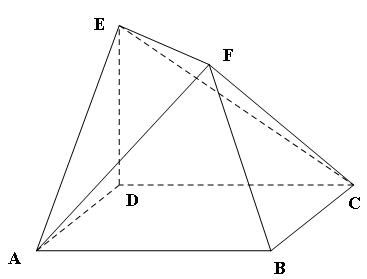
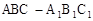 中,
中,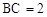 ,
,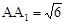 ,D、E分别是
,D、E分别是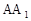 、
、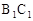 的中点,
的中点,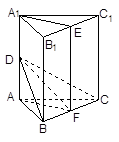
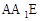 ⊥面BCD;
⊥面BCD;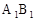 与平面BCD所成的角.
与平面BCD所成的角.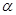 ,
,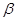 ,
,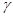 是三个两两不重合的平面,给出下列四个命题:
是三个两两不重合的平面,给出下列四个命题: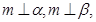 则
则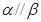 ;
;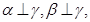 则
则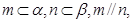 则
则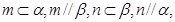 则
则
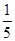


 分别是正方体
分别是正方体 的棱
的棱 的中点,点
的中点,点 分别是线段
分别是线段 与
与 上的点,则与平面
上的点,则与平面 垂直的直线
垂直的直线 有( )
有( )
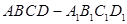 中,线段
中,线段 上(不包括端点)各有一点
上(不包括端点)各有一点 ,且
,且 ,下列说法中,不正确的是( )
,下列说法中,不正确的是( ) 四点共面
四点共面 与平面
与平面 所成的角为定值
所成的角为定值
 的大小为
的大小为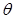 ,则
,则 的最小值为
的最小值为