题目内容
已知函数![]() 在
在![]() 处有极值
处有极值![]() .
.
(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)判断函数![]() 的单调性并求出单调区间.
的单调性并求出单调区间.
(Ⅰ)![]() ,
,![]() (Ⅱ)
(Ⅱ)![]() 的单调减区间是
的单调减区间是![]() ,单调增区间是
,单调增区间是![]()
解析:
(Ⅰ)因为函数![]() ,
,
所以![]() .………………………………………………………………2分
.………………………………………………………………2分
又函数![]() 在
在![]() 处有极值
处有极值![]() ,
,
所以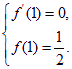 即
即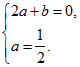
可得![]() ,
,![]() .…………………………………………………………6分
.…………………………………………………………6分
(Ⅱ)由(Ⅰ)可知![]() ,其定义域是
,其定义域是![]() ,
,
且![]() .………………………………………………10分
.………………………………………………10分
当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
| 极小值 |
|
所以函数![]() 的单调减区间是
的单调减区间是![]() ,单调增区间是
,单调增区间是![]() .…………………13分
.…………………13分

练习册系列答案
相关题目
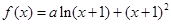 在
在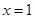 处有极值.
处有极值.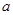 值;
值;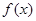 的单调区间;
的单调区间;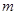 ,使得不等式
,使得不等式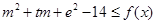 对任意
对任意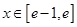 及
及
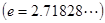
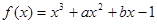 在
在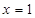 处有极值
处有极值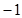 。
。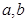 的值;
的值;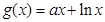 的单调区间。
的单调区间。 在
在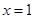 处有极值
处有极值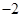 .
.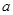 、
、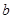 ;
; 与
与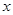 轴所包围的面积。
轴所包围的面积。