题目内容
(本小题满分12分)
已知函数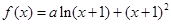 在
在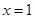 处有极值.
处有极值.
(Ⅰ)求实数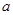 值;
值;
(Ⅱ)求函数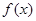 的单调区间;
的单调区间;
(Ⅲ)试问是否存在实数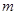 ,使得不等式
,使得不等式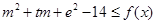 对任意
对任意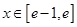 及
及
恒成立?若存在,求出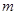 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.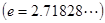
【答案】
(Ⅰ)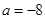 (Ⅱ)
(Ⅱ)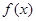 的单调减区间为
的单调减区间为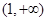 ,
,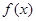 的单调减区间为
的单调减区间为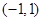 (Ⅲ)存在
(Ⅲ)存在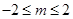 ,使得不等式
,使得不等式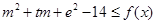 对任意
对任意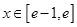 及
及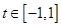
恒成立
【解析】
试题分析:解:解:(Ⅰ)因为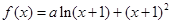 ,
,
所以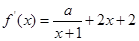 . ……2分
. ……2分
由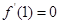 ,可得
,可得 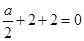 ,
,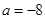 .
.
经检验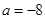 时,函数
时,函数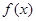 在
在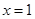 处取得极值,
处取得极值,
所以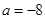 . ………4分
. ………4分
(Ⅱ)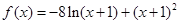 ,
,
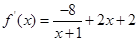
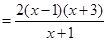 . ……6分
. ……6分
而函数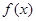 的定义域为
的定义域为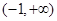 ,
,
当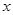 变化时,
变化时,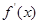 ,
,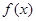 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
- |
0 |
+ |
|
|
↘ |
极小值 |
↗ |
由表可知,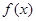 的单调减区间为
的单调减区间为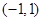 ,
,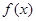 的单调减区间为
的单调减区间为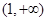 .……9分
.……9分
(3)∵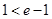 ,
,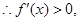
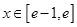 时,
时,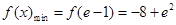 …10分
…10分
不等式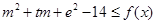 对任意
对任意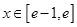 及
及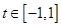 恒成立,即
恒成立,即
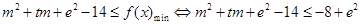 ,
,
即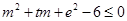 对
对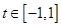 恒成立, …12分
恒成立, …12分
令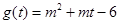 ,
,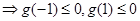
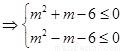 ,
,
解得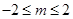 为所求. …14分
为所求. …14分
考点:函数的极值;函数的导数与单调性的关系;不等式的性质。
点评:本题三个小题相扣,前一小题都是解决下个小题的基础。

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目




