题目内容
已知曲线C的极坐标方程为 .
.
(1)若直线 过原点,且被曲线C截得弦长最短,求此时直线
过原点,且被曲线C截得弦长最短,求此时直线 的标准形式的参数方程;
的标准形式的参数方程;
(2) 是曲线C上的动点,求
是曲线C上的动点,求 的最大值.
的最大值.
(1) (t为参数)(2)
(t为参数)(2)
解析试题分析:(1)化曲线C的极坐标方程为直角坐标方程,求得圆心C(1,-1),要使直线l过原点,且被曲线C截得弦长最短,则OC⊥l,故可求;(2)设M( ,
, ),θ为参数,则x+y=
),θ为参数,则x+y= =
= ,故可求x+y的最大值.
,故可求x+y的最大值.
试题解析: (1)∵曲线C的极坐标方程为: ∴ρ2-2ρcosθ+2ρsinθ-2=0∴x2+y2-2x+2y-2=0,∴(x-1)2+(y+1)2=4 ∴圆心C(1,-1),∴kOC=-1,
∴ρ2-2ρcosθ+2ρsinθ-2=0∴x2+y2-2x+2y-2=0,∴(x-1)2+(y+1)2=4 ∴圆心C(1,-1),∴kOC=-1,
∵直线l过原点,且被曲线C截得弦长最短,∴直线l斜率为1,
∴参数方程为 (t为参数)
(t为参数)
(2)设M( ,
, )(θ为参数),则x+y=
)(θ为参数),则x+y= =
=
∵?1≤sin(θ+ )≤1∴
)≤1∴ ,所以x+y的最大值为
,所以x+y的最大值为 .
.
考点:1.极坐标方程;2.直线的参数方程;3.圆的参数方程.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 (
( 为参数)的倾斜角为__________.
为参数)的倾斜角为__________. 的离心率是 .
的离心率是 . 上的动点
上的动点 是坐标为
是坐标为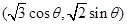 .
.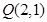 作曲线
作曲线 、
、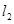 ,证明
,证明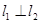 .
. 中,直线
中,直线 经过点P(0,1),曲线
经过点P(0,1),曲线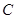 的方程为
的方程为 ,若直线
,若直线 ,
, 两点,求
两点,求 的值.
的值. ,直线
,直线 :
: (
( 为参数).
为参数). 的参数方程,直线
的参数方程,直线 作与
作与 的直线,交
的直线,交 ,
, 的最大值与最小值.
的最大值与最小值. 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),若以直角坐标系的原点
为参数),若以直角坐标系的原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标,曲线
轴的正半轴为极轴建立极坐标,曲线 的极坐标方程为
的极坐标方程为 (其中
(其中 为常数).
为常数). 时,求曲线
时,求曲线 ,它们的夹角为
,它们的夹角为 ,如图所示,点C在以
,如图所示,点C在以 为圆心的圆弧AB上运动,若
为圆心的圆弧AB上运动,若 ,其中
,其中 ,则
,则 的最大值是 .
的最大值是 .
 (t为参数),若点P(m,2)在曲线C上,求m的值.
(t为参数),若点P(m,2)在曲线C上,求m的值.