题目内容
已知P是椭圆 上不同于左顶点A、右顶点B的任意一点,直线PA交直线l:x=4于点M,直线PB交直线l于点N,记直线PA,PB的斜率分别为k1,k2.
上不同于左顶点A、右顶点B的任意一点,直线PA交直线l:x=4于点M,直线PB交直线l于点N,记直线PA,PB的斜率分别为k1,k2.(1)求k1•k2的值;
(2)求证以MN为直径的圆恒经过两定点.
【答案】分析:(1)A(-2,0),B(2,0),设P(x,y),故 ,由此能求出k1•k2的值.
,由此能求出k1•k2的值.
(2)设 ,所以y1y2=-9,以MN为直径的圆的方程为(x-4)(x-4)+(y-y1)(y-y2)=0,令y=0,解得x=1或x=7.由此能导出以MN为直径的圆恒过x轴上的两定点(1,0)和(7,0).
,所以y1y2=-9,以MN为直径的圆的方程为(x-4)(x-4)+(y-y1)(y-y2)=0,令y=0,解得x=1或x=7.由此能导出以MN为直径的圆恒过x轴上的两定点(1,0)和(7,0).
解答:解:(1)A(-2,0),B(2,0),
设P(x,y),
故 ,
,
即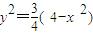 ,
,
 .
.
(2)设 ,所以y1y2=-9,
,所以y1y2=-9,
以MN为直径的圆的方程为(x-4)(x-4)+(y-y1)(y-y2)=0,
令y=0,得(x-4)2+(-y1)(-y2)=0,解得x=1或x=7.
∴以MN为直径的圆恒过x轴上的两定点(1,0)和(7,0).
点评:本题考查求k1•k2的值和求证以MN为直径的圆恒经过两定点.解题时要认真审题,注意挖掘题设中的隐条件,灵活运用椭圆的性质,合理地进行等价转化.
 ,由此能求出k1•k2的值.
,由此能求出k1•k2的值.(2)设
 ,所以y1y2=-9,以MN为直径的圆的方程为(x-4)(x-4)+(y-y1)(y-y2)=0,令y=0,解得x=1或x=7.由此能导出以MN为直径的圆恒过x轴上的两定点(1,0)和(7,0).
,所以y1y2=-9,以MN为直径的圆的方程为(x-4)(x-4)+(y-y1)(y-y2)=0,令y=0,解得x=1或x=7.由此能导出以MN为直径的圆恒过x轴上的两定点(1,0)和(7,0).解答:解:(1)A(-2,0),B(2,0),
设P(x,y),
故
 ,
,即
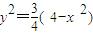 ,
, .
.(2)设
 ,所以y1y2=-9,
,所以y1y2=-9,以MN为直径的圆的方程为(x-4)(x-4)+(y-y1)(y-y2)=0,
令y=0,得(x-4)2+(-y1)(-y2)=0,解得x=1或x=7.
∴以MN为直径的圆恒过x轴上的两定点(1,0)和(7,0).
点评:本题考查求k1•k2的值和求证以MN为直径的圆恒经过两定点.解题时要认真审题,注意挖掘题设中的隐条件,灵活运用椭圆的性质,合理地进行等价转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 上不同于左顶点A、右顶点B的任意一点,记直线PA,PB的斜率分别为k1,k2,则k1•k2的值为________.
上不同于左顶点A、右顶点B的任意一点,记直线PA,PB的斜率分别为k1,k2,则k1•k2的值为________. 上不同于左顶点A、右顶点B的任意一点,记直线PA,PB的斜率分别为k1,k2,则k1•k2的值为 .
上不同于左顶点A、右顶点B的任意一点,记直线PA,PB的斜率分别为k1,k2,则k1•k2的值为 . 上不同于左顶点A、右顶点B的任意一点,记直线PA,PB的斜率分别为k1,k2,则k1·k2的值为( )。
上不同于左顶点A、右顶点B的任意一点,记直线PA,PB的斜率分别为k1,k2,则k1·k2的值为( )。