题目内容
tan2012°∈
- A.
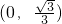
- B.
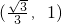
- C.
- D.
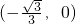
B
分析：将2012°变形为11×180°+32°，利用诱导公式tan（n•180°+α）=tanα化简，再由30°＜32°＜45°，且正切函数在（0，90°）上为增函数，得出tan32°的范围，即可确定出tan2012°的范围．
解答：tan2012°=tan（1980°+32°）=tan（11×180°+32°）=tan32°，
∵30°＜32°＜45°，且正切函数在（0，90°）上为增函数，
∴tan30°＜tan32°＜tan45°，即
＜tan32°＜1，
则tan2012°∈（，1）．
故选B
点评：此题考查了运用诱导公式化简求值，特殊角的三角函数值，以及正切函数的增减性，熟练掌握诱导公式是解本题的关键．
分析：将2012°变形为11×180°+32°，利用诱导公式tan（n•180°+α）=tanα化简，再由30°＜32°＜45°，且正切函数在（0，90°）上为增函数，得出tan32°的范围，即可确定出tan2012°的范围．
解答：tan2012°=tan（1980°+32°）=tan（11×180°+32°）=tan32°，
∵30°＜32°＜45°，且正切函数在（0，90°）上为增函数，
∴tan30°＜tan32°＜tan45°，即
＜tan32°＜1，则tan2012°∈（
，1）．故选B
点评：此题考查了运用诱导公式化简求值，特殊角的三角函数值，以及正切函数的增减性，熟练掌握诱导公式是解本题的关键．
练习册系列答案
中考解读考点精练系列答案
相关题目