题目内容
(本小题满分14分)
已知一非零向量列 满足:
满足: ,
,
 .
.
(1)证明: 是等比数列;
是等比数列;
(2)设 是
是 的夹角
的夹角 ,
, =
= ,
, ,求
,求 ;
;
(3)设
 ,问数列
,问数列 中是否存在最小项?若存在,求出最小值;若不存在,请说明理由.
中是否存在最小项?若存在,求出最小值;若不存在,请说明理由.
已知一非零向量列
 满足:
满足: ,
,
 .
. (1)证明:
 是等比数列;
是等比数列;(2)设
 是
是 的夹角
的夹角 ,
, =
= ,
, ,求
,求 ;
;(3)设

 ,问数列
,问数列 中是否存在最小项?若存在,求出最小值;若不存在,请说明理由.
中是否存在最小项?若存在,求出最小值;若不存在,请说明理由. 解:(1)
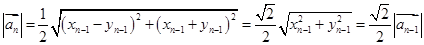
 ………3分
………3分∴数列
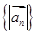 是以公比为
是以公比为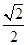 ,首项为
,首项为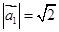 的等比数列;…………………………4分
的等比数列;…………………………4分(2)∵

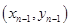
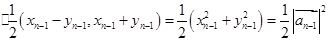 ,
,∴
 =
=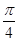 ,…………………………………………………………………………………………6分
,…………………………………………………………………………………………6分∴
 =
=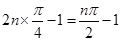 ,……………………………………………………………………7分
,……………………………………………………………………7分∴
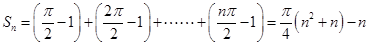 。…………………………9分
。…………………………9分(3)假设存在最小项,设为
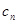 ,
,∵
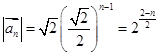 ,………………………………………………………………10分
,………………………………………………………………10分∴
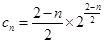 ,…………………………………………………………………………11分
,…………………………………………………………………………11分由
 得当
得当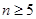 时,
时,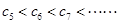 ;
;由
 得当
得当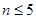 时,
时,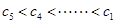 ;……………………………………………13分
;……………………………………………13分故存在最小项为
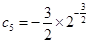 。 …………………………………………………………14分
。 …………………………………………………………14分略

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
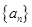 的前
的前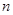 项和为
项和为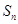 ,满足
,满足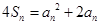 ,
,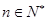 .(Ⅰ)求数列
.(Ⅰ)求数列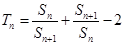 ,证明:
,证明: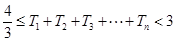
 中,a1=3,前三项和为21,则a3 + a4 + a5 = ( )
中,a1=3,前三项和为21,则a3 + a4 + a5 = ( )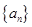 的前n项和为Sn,若
的前n项和为Sn,若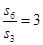 ,则
,则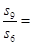 ( )
( )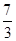
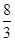
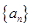 ,
,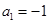 ,
,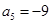 ,则
,则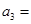 _____________.
_____________. 若存在两项
若存在两项 、
、 使得
使得 ,则
,则 的最小值为
的最小值为  是等比数列,且
是等比数列,且 ,
, ,
, ,则数列
,则数列 的公比
的公比 _________
_________ 的前
的前 项和为
项和为 ,且
,且 ,
, 且
且
