题目内容
设双曲线
分析:由两点式得直线l的方程,再由双曲线中a、b、c的关系及原点到直线l的距离建立等式,从而求出![]() .
.
解:由l过两点(a,0)、(0,b),得l的方程为bx+ay-ab=0.
由原点到l的距离为![]() c,得
c,得![]() c.
c.
将b=![]() 代入,平方后整理,得16(
代入,平方后整理,得16(![]() )2-16×
)2-16×![]() +3=0.令
+3=0.令![]() =x,
=x,
则16x2-16x+3=0,解得x=![]() 或x=
或x=![]() .又e=
.又e=![]() ,有e=
,有e=![]() .故e=
.故e=![]() 或e=2.
或e=2.
因0<a<b,故e=![]() =
=![]() =
=![]() >
>![]() ,
,
所以应舍去e=![]() ,故所求离心率e=2.
,故所求离心率e=2.
点评:此题易得出错误答案e=2或e=![]() ,其原因是未注意到题设条件0<a<b,从而离心率e>2,而
,其原因是未注意到题设条件0<a<b,从而离心率e>2,而![]() <2,应舍去.
<2,应舍去.

练习册系列答案
相关题目
 =1(a>0,b>0)的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为
=1(a>0,b>0)的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为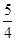 B.5 C.
B.5 C. D.
D.