Question

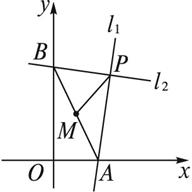
过点P(2,4)作两条互相垂直的直线l_１，l_２，若l_１交x轴于A点，

l₂ 交y轴于B点，求线段AB的中点M的轨迹方程．

Answer 1

点M的轨迹方程是x+2y-5=0．

解析:

设点M的坐标为(x,y),

∵M为线段AB的中点，∴A的坐标为(2x,0)，B的坐标为(0，2y)，

∵l_１⊥l_２，且l_１、l_２过点P(2，4)，

∴PA⊥PB,k_PA·ｋ_ＰＢ＝－１．

而

整理，得x+2y-5=0(x≠1)

∵当x=1时，A、B的坐标分别为(2，0)、(0，4)．

∴线段AB的中点坐标是(1，2)，它满足方程x+2y-5=0，

综上所述，点M的轨迹方程是x+2y-5=0．