题目内容
函数 在[0,2]上单调递增,且函数
在[0,2]上单调递增,且函数 是偶函数,则下列结论成立的是( )
是偶函数,则下列结论成立的是( )
A.f(1)<f(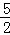 )<f(
)<f(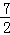 )
)
B.f(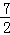 )<f(1)<f(
)<f(1)<f( )
)
C.f(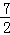 )<f(
)<f( )<f(1)
)<f(1)
D.f( )<f(1)<f(
)<f(1)<f(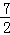 )
)
B
【解析】
试题分析:由函数 为偶函数,得
为偶函数,得 的图像关于直线
的图像关于直线 对称,又因为
对称,又因为 在[0,2]
在[0,2]
上单调递增,所以其在 上是减函数,从而得自变量距离
上是减函数,从而得自变量距离 越近,函数值就越大,从而得结果.
越近,函数值就越大,从而得结果.
考点:函数图像的变换,函数的奇偶性,以及比较函数值的大小.

练习册系列答案
相关题目
 虚数单位,则复数
虚数单位,则复数 的虚部为 ( ).
的虚部为 ( ). B.
B. C.
C. D.
D.
 .
. 的奇偶性,并加以证明;[来(2)用定义证明函数
的奇偶性,并加以证明;[来(2)用定义证明函数 上为增函数.
上为增函数.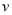 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度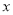 (单位:辆/小时)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当
(单位:辆/小时)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当 时,车流速度
时,车流速度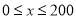 时,求函数
时,求函数 的表达式;
的表达式;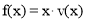 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时) 的值域为________.
的值域为________. 分别为椭圆
分别为椭圆 的左、右两个焦点.
的左、右两个焦点. 上的点
上的点 到
到 两点的距离之和等于4,求椭圆
两点的距离之和等于4,求椭圆 是(1)中所得椭圆上的动点,
是(1)中所得椭圆上的动点, ,求
,求 的最大值.
的最大值.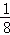 B.
B.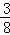 C.
C. D.
D.