题目内容
(本小题10分)设 分别为椭圆
分别为椭圆 的左、右两个焦点.
的左、右两个焦点.
(1)若椭圆 上的点
上的点 到
到 两点的距离之和等于4,求椭圆
两点的距离之和等于4,求椭圆 的方程和焦点坐标;
的方程和焦点坐标;
(2)设点 是(1)中所得椭圆上的动点,
是(1)中所得椭圆上的动点, ,求
,求 的最大值.
的最大值.
(1)椭圆方程 ,焦点
,焦点 ,
,
(2)当 时,
时, ,即:
,即:
【解析】
试题分析:依据椭圆的定义椭圆 上的点
上的点 到
到 两点的距离之和为
两点的距离之和为 ,
, 在椭圆
在椭圆 上,代入求出
上,代入求出 ,得出椭圆
,得出椭圆 的方程和焦点坐标,第二步设设
的方程和焦点坐标,第二步设设 是椭圆上任意一点,则
是椭圆上任意一点,则 ,求出
,求出 的表达式,消去
的表达式,消去 ,得到关于
,得到关于 的二次三项式,经过配方得出抛物线的顶点式,画出抛物线,因
的二次三项式,经过配方得出抛物线的顶点式,画出抛物线,因 ,得出最大值,再给出
,得出最大值,再给出 的最大值.
的最大值.
试题解析:(1)依据椭圆的定义 ,
, 在椭圆
在椭圆 上,
上, ,得椭圆方程
,得椭圆方程 ,焦点
,焦点 ,
, .
.
(2)设 是椭圆上任意一点,则
是椭圆上任意一点,则 ,(
,( ),
),


 ,
, ,
,
则当 时,
时, ,即:
,即:
考点:1.椭圆的定义和标准方程;(2)建立函数关系,用减元法消去 ,得出关于
,得出关于 的二次函数;3.利用函数思想求最值;
的二次函数;3.利用函数思想求最值;

练习册系列答案
相关题目

 在[0,2]上单调递增,且函数
在[0,2]上单调递增,且函数 是偶函数,则下列结论成立的是( )
是偶函数,则下列结论成立的是( )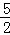 )<f(
)<f(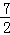 )
)  )
)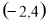 且在两坐标轴上截距的绝对值相等的直线有( )
且在两坐标轴上截距的绝对值相等的直线有( )
 的共轭复数是 .
的共轭复数是 . ,则
,则 ”的逆否命题为“若
”的逆否命题为“若 ,则
,则 ”.
”. ,
, ,则“
,则“ ”为:
”为: .
. ”是“
”是“ ”的充分不必要条件.
”的充分不必要条件. 或
或 ;q:
;q: 或
或 ,则
,则 是
是 的必要不充分条件
的必要不充分条件 的解集是区间
的解集是区间 的子集,则实数
的子集,则实数 的取值范围为
的取值范围为