题目内容
已知函数 (x∈R).
(x∈R).
(1)求函数f(x)的最小正周期;
(3)当x为何值时,f(x)的值最大?最大值是多少?
(本小题满分12分)
解:(1)由题得, (6分)
(6分)
∴周期T=π(8分)
(2)当 时,此时
时,此时 ,
, (10分)
(10分)
有f(x)最大值=2 (12分)
分析:(1)通过两角差的正弦函数,化简函数的表达式为一个角的一个三角函数的形式,利用周期公式求函数f(x)的最小正周期;
(3)借助正弦函数的有界性,求出x的值,以及f(x)的值最大,最大值的值.
点评:本题考查三角函数的化简求值,周期、最值以及两角差的正弦函数的应用,考查计算能力.
解:(1)由题得,
 (6分)
(6分)∴周期T=π(8分)
(2)当
 时,此时
时,此时 ,
, (10分)
(10分)有f(x)最大值=2 (12分)
分析:(1)通过两角差的正弦函数,化简函数的表达式为一个角的一个三角函数的形式,利用周期公式求函数f(x)的最小正周期;
(3)借助正弦函数的有界性,求出x的值,以及f(x)的值最大,最大值的值.
点评:本题考查三角函数的化简求值,周期、最值以及两角差的正弦函数的应用,考查计算能力.

练习册系列答案
相关题目
 (x∈R).若
(x∈R).若 ,
, .求cos2x的值.
.求cos2x的值. ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.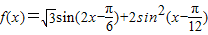 (x∈R).
(x∈R). ,x∈R
,x∈R
 ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.