题目内容
已知函数
（x∈R）．若
，
．求cos2x的值．
【答案】分析：将函数化简为y=Asin（ωx+φ）的形式，把x代入化简后的函数解析式可得到sin（2x+
）=
，再根据x的范围可求出cos（2x+
）的值，利用cos2x=cos[（2x+
）-
]，我们就可以得出结论
解答：解：函数
=
（2sinxcosx）+（2cos2x-1）=
sin2x+cos2x=2sin（2x+
）
因为f（x）=
，所以sin（2x+
）=
由x∈[
，
]，得2x+
∈[
，
]
从而cos（2x+
）=-
=-
．
所以cos2x=cos[（2x+
）-
]=cos（2x+
）cos
+sin（2x+
）sin
=
．
点评：本题主要考查二倍角的正弦与余弦、辅助角公式、函数y=Asin（ωx+φ）的性质、同角三角函数的基本关系、两角差的余弦等基础知识，利用2x=（2x+
）-
是我们思维的亮点所在．
）=，再根据x的范围可求出cos（2x+）的值，利用cos2x=cos[（2x+）-]，我们就可以得出结论解答：解：函数
=（2sinxcosx）+（2cos2x-1）=sin2x+cos2x=2sin（2x+）因为f（x）=
，所以sin（2x+）=由x∈[
，]，得2x+∈[，]从而cos（2x+
）=-=-．所以cos2x=cos[（2x+
）-]=cos（2x+）cos+sin（2x+）sin=．点评：本题主要考查二倍角的正弦与余弦、辅助角公式、函数y=Asin（ωx+φ）的性质、同角三角函数的基本关系、两角差的余弦等基础知识，利用2x=（2x+
）-是我们思维的亮点所在． 
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，x∈R，且
，
，
，求cos（α+β）的值．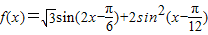
（x∈R）．
，x∈R
，x∈R，且
，
，
，求cos（α+β）的值．