题目内容
已知函数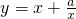 有如下性质:如果常数a>0,那么该函数在
有如下性质:如果常数a>0,那么该函数在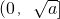 上是减函数,在
上是减函数,在 上是增函数,
上是增函数,
(1)如果函数 的值域是[6,+∞),求实数m的值;
的值域是[6,+∞),求实数m的值;
(2)研究函数 (常数a>0)在定义域内的单调性,并说明理由;
(常数a>0)在定义域内的单调性,并说明理由;
(3)若把函数 (常数a>0)在[1,2]上的最小值记为g(a),求g(a)的表达式.
(常数a>0)在[1,2]上的最小值记为g(a),求g(a)的表达式.
解:(1)由已知,函数 在
在 上是减函数,在
上是减函数,在 上是增函数,
上是增函数,
∴
∴ ,3m=9
,3m=9
因此m=2.
(2)根据题意, ,x≠0,
,x≠0,
令t=x2,x≠0,则t>0,
故y=t+ ,那么该函数在
,那么该函数在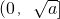 上是减函数,在
上是减函数,在 上是增函数,
上是增函数,
而t=x2在(0,+∞)单调递增,在(-∞,0)单调递减;
由复合函数的单调性,
当 时,t=x2递增,t在
时,t=x2递增,t在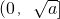 上,则y=t+
上,则y=t+ 是减函数,故f(x)在
是减函数,故f(x)在 上是减函数,
上是减函数,
当x∈ 时,t=x2递增,t在
时,t=x2递增,t在 上,则y=t+
上,则y=t+ 是增函数,故f(x)在
是增函数,故f(x)在 上是增函数,
上是增函数,
当x∈ ,t=x2递减,t在
,t=x2递减,t在 上,则y=t+
上,则y=t+ 是增函数,故f(x)在
是增函数,故f(x)在 上是减函数,
上是减函数,
当x∈ ,t=x2递减,t在
,t=x2递减,t在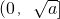 上,则y=t+
上,则y=t+ 是减函数,故f(x)在
是减函数,故f(x)在 上是增函数,
上是增函数,
因此f(x)在 ,
, 上是减函数,在
上是减函数,在 ,
, 上是增函数.
上是增函数.
(3)由(2)知,f(x)在 上是减函数,在
上是减函数,在 上是增函数,
上是增函数,
于是当 ,即a>16时,
,即a>16时, ,
,
当 ,即1≤a≤16时,
,即1≤a≤16时, ,
,
当 ,即0<a<1时,g(a)=f(1)=1+a.
,即0<a<1时,g(a)=f(1)=1+a.
因此 .
.
分析:(1)根据题意,易得由已知,函数 在
在 上是减函数,在
上是减函数,在 上是增函数,则该函数当x=
上是增函数,则该函数当x= 时,取得最小值,有题意知其最小值为6,可得
时,取得最小值,有题意知其最小值为6,可得 ,解可得答案;
,解可得答案;
(2)根据题意,求得 的定义域为x≠0,再令t=x2,x≠0,有t>0,则y=t+
的定义域为x≠0,再令t=x2,x≠0,有t>0,则y=t+ ,那么该函数在
,那么该函数在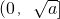 上是减函数,在
上是减函数,在 上是增函数,而t=x2在(0,+∞)单调递增,在(-∞,0)单调递减;
上是增函数,而t=x2在(0,+∞)单调递增,在(-∞,0)单调递减;
由复合函数的单调性分析可得答案;
(3)由(2)的结论,分可 、
、 、
、 三种情况讨论,分别得到g(a)的表达式,即可得答案.
三种情况讨论,分别得到g(a)的表达式,即可得答案.
点评:本题考查函数单调性的运用,解题的关键在于紧扣题干所给函数的单调性的性质,并利用其解题.
 在
在 上是减函数,在
上是减函数,在 上是增函数,
上是增函数,∴

∴
 ,3m=9
,3m=9因此m=2.
(2)根据题意,
 ,x≠0,
,x≠0,令t=x2,x≠0,则t>0,
故y=t+
 ,那么该函数在
,那么该函数在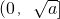 上是减函数,在
上是减函数,在 上是增函数,
上是增函数,而t=x2在(0,+∞)单调递增,在(-∞,0)单调递减;
由复合函数的单调性,
当
 时,t=x2递增,t在
时,t=x2递增,t在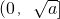 上,则y=t+
上,则y=t+ 是减函数,故f(x)在
是减函数,故f(x)在 上是减函数,
上是减函数,当x∈
 时,t=x2递增,t在
时,t=x2递增,t在 上,则y=t+
上,则y=t+ 是增函数,故f(x)在
是增函数,故f(x)在 上是增函数,
上是增函数,当x∈
 ,t=x2递减,t在
,t=x2递减,t在 上,则y=t+
上,则y=t+ 是增函数,故f(x)在
是增函数,故f(x)在 上是减函数,
上是减函数,当x∈
 ,t=x2递减,t在
,t=x2递减,t在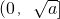 上,则y=t+
上,则y=t+ 是减函数,故f(x)在
是减函数,故f(x)在 上是增函数,
上是增函数,因此f(x)在
 ,
, 上是减函数,在
上是减函数,在 ,
, 上是增函数.
上是增函数.(3)由(2)知,f(x)在
 上是减函数,在
上是减函数,在 上是增函数,
上是增函数,于是当
 ,即a>16时,
,即a>16时, ,
,当
 ,即1≤a≤16时,
,即1≤a≤16时, ,
,当
 ,即0<a<1时,g(a)=f(1)=1+a.
,即0<a<1时,g(a)=f(1)=1+a. 因此
 .
.分析:(1)根据题意,易得由已知,函数
 在
在 上是减函数,在
上是减函数,在 上是增函数,则该函数当x=
上是增函数,则该函数当x= 时,取得最小值,有题意知其最小值为6,可得
时,取得最小值,有题意知其最小值为6,可得 ,解可得答案;
,解可得答案;(2)根据题意,求得
 的定义域为x≠0,再令t=x2,x≠0,有t>0,则y=t+
的定义域为x≠0,再令t=x2,x≠0,有t>0,则y=t+ ,那么该函数在
,那么该函数在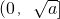 上是减函数,在
上是减函数,在 上是增函数,而t=x2在(0,+∞)单调递增,在(-∞,0)单调递减;
上是增函数,而t=x2在(0,+∞)单调递增,在(-∞,0)单调递减;由复合函数的单调性分析可得答案;
(3)由(2)的结论,分可
 、
、 、
、 三种情况讨论,分别得到g(a)的表达式,即可得答案.
三种情况讨论,分别得到g(a)的表达式,即可得答案.点评:本题考查函数单调性的运用,解题的关键在于紧扣题干所给函数的单调性的性质,并利用其解题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
 有如下性质:如果常数
有如下性质:如果常数 ,那么该函数在
,那么该函数在 上是减函数,在
上是减函数,在 上是增函数。
上是增函数。 在
在 上是减函数,在
上是减函数,在 上是增函数,求
上是增函数,求 的值。
的值。 ,求函数
,求函数 的最大值和最小值;
的最大值和最小值; 有如下性质:如果常数
有如下性质:如果常数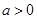 ,那么该函数在
,那么该函数在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数; 在
在 上是减函数,在
上是减函数,在 上是增函数,求
上是增函数,求 的值;
的值;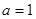 时,试用函数单调性的定义证明函数f(x)在
时,试用函数单调性的定义证明函数f(x)在 上是减函数。
上是减函数。 ,求函数
,求函数 的最大值和最小值;
的最大值和最小值;