Question

（本题12分）已知函数有如下性质：如果常数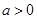，那么该函数在上是减函数，在上是增函数；

（1）如果函数在上是减函数，在上是增函数，求的值；

（2）当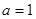时，试用函数单调性的定义证明函数f(x)在上是减函数。

（3）设常数，求函数的最大值和最小值；

 

Answer 1

【答案】

 

（1）b=4

（2）当1≤c≤3时, 函数f(x)的最大值是f(3)=3+；

当3<c≤9时, 函数f(x)的最大值是f(1)=1+c.

【解析】解. (1) 由已知得=4, ∴b=4.

 (2)设,∈，且<，  ∵－,

由,∈，<得0<<1,1->0，故－>0 ,于是－>0,

即 > .∴= 在上是减函数.

 (3) ∵c∈[1,9], ∴∈[1,3], 于是,当x=时, 函数f(x)=x+取得最小值2.

而f(1)－f(3)=,所以：

当1≤c≤3时, 函数f(x)的最大值是f(3)=3+；

当3<c≤9时, 函数f(x)的最大值是f(1)=1+c.