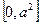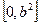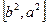题目内容
(本题满分13分)
设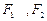 分别是椭圆C:
分别是椭圆C: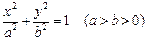 的左右焦点,
的左右焦点,
(1)设椭圆C上的点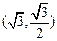 到
到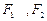 两点距离之和等于4,写出椭圆C的方程和焦点坐标。
两点距离之和等于4,写出椭圆C的方程和焦点坐标。
(2)设K是(1)中所得椭圆上的动点,求线段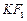 的中点B的轨迹方程。
的中点B的轨迹方程。
(3 )设点P是椭圆C 上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线PM ,PN的斜率都存在,并记为
)设点P是椭圆C 上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线PM ,PN的斜率都存在,并记为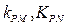 试探究
试探究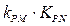 的值是否与点P及直线L有关,并证明你的结论。
的值是否与点P及直线L有关,并证明你的结论。
设
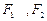 分别是椭圆C:
分别是椭圆C: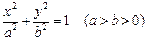 的左右焦点,
的左右焦点,(1)设椭圆C上的点
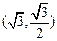 到
到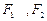 两点距离之和等于4,写出椭圆C的方程和焦点坐标。
两点距离之和等于4,写出椭圆C的方程和焦点坐标。(2)设K是(1)中所得椭圆上的动点,求线段
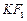 的中点B的轨迹方程。
的中点B的轨迹方程。(3
 )设点P是椭圆C 上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线PM ,PN的斜率都存在,并记为
)设点P是椭圆C 上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线PM ,PN的斜率都存在,并记为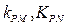 试探究
试探究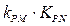 的值是否与点P及直线L有关,并证明你的结论。
的值是否与点P及直线L有关,并证明你的结论。(1)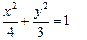 焦点坐标分别为(-1,0) ,(1,0)
焦点坐标分别为(-1,0) ,(1,0)
(2)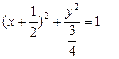
(3)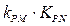 的值与点P的位置无关,同时与直线L无关
的值与点P的位置无关,同时与直线L无关
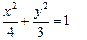 焦点坐标分别为(-1,0) ,(1,0)
焦点坐标分别为(-1,0) ,(1,0)(2)
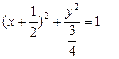
(3)
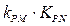 的值与点P的位置无关,同时与直线L无关
的值与点P的位置无关,同时与直线L无关解:(1)由于点
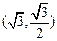 在椭圆上,
在椭圆上,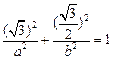 2
2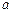 ="4, "
="4, " 椭圆C的方程为
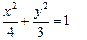
焦点坐标分别为(-1,0) ,(1,0)-----------3分
(2)设
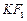 的中点为B(x, y)则点
的中点为B(x, y)则点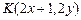
把K的坐标代入椭圆
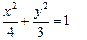 中得
中得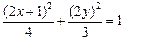
线段
 的中点B的轨迹方程为
的中点B的轨迹方程为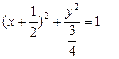 ----------8
----------8 分
分(3)过原点的直线L与椭圆相交的两点M,N关
 于坐标原点对称
于坐标原点对称 设
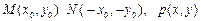
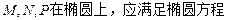
得
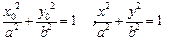
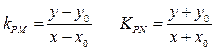
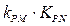 =
=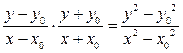 =
=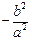
故:
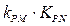 的值与点P的位置无关,同时与直线L无关. 13分
的值与点P的位置无关,同时与直线L无关. 13分
练习册系列答案
相关题目
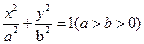 过点
过点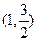 ,且长轴长等于4.
,且长轴长等于4.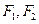 是椭圆C的两个焦点,⊙O是以F1F2为直径的圆,直线l: y=kx+m与⊙O相切,并与椭圆C交于不同的两点A、B,若
是椭圆C的两个焦点,⊙O是以F1F2为直径的圆,直线l: y=kx+m与⊙O相切,并与椭圆C交于不同的两点A、B,若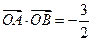 ,求
,求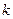 的值.
的值.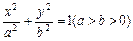 的离心率为
的离心率为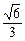 ,椭圆C上任意一点到椭圆两焦点的距离和为6.
,椭圆C上任意一点到椭圆两焦点的距离和为6.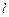 :
: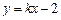 与椭圆C交于A,B两点,点P(0,1),且
与椭圆C交于A,B两点,点P(0,1),且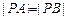 ,求直线
,求直线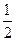 ,且椭圆E上一点到两个焦点距离之和为4;
,且椭圆E上一点到两个焦点距离之和为4;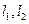 是过点P(0,2)且互相垂直的两条直线,
是过点P(0,2)且互相垂直的两条直线,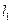 交E于A,B两点,
交E于A,B两点,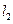 交E交C,D两点,AB,CD的中点分别为M,N。
交E交C,D两点,AB,CD的中点分别为M,N。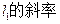 k的取值范围;
k的取值范围;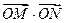 的取值范围。
的取值范围。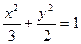 的左、右焦点分别为F1、F2.过F1的直线交椭圆于B、D两点,过F2的直线交椭圆于A、C两点,且AC⊥BD,垂足为P.
的左、右焦点分别为F1、F2.过F1的直线交椭圆于B、D两点,过F2的直线交椭圆于A、C两点,且AC⊥BD,垂足为P.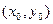 ,证明:
,证明: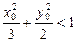 ;
;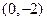 、
、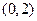 ,并且经过点
,并且经过点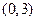 的椭圆方程是
的椭圆方程是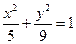 B.
B.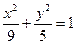 C.
C.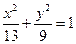 D.
D.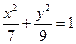

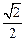

 的中心在原点,长轴在
的中心在原点,长轴在 轴上,离心率为
轴上,离心率为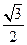 ,且
,且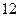 ,则椭圆
,则椭圆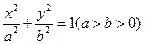 上任意一点,
上任意一点,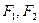 是其两个焦点,则
是其两个焦点,则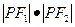 的取值范围是( )
的取值范围是( )