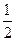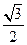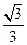题目内容
(本小题满分13分)
已知椭圆E的中心在坐标原点,焦点在x轴上,离心率为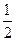 ,且椭圆E上一点到两个焦点距离之和为4;
,且椭圆E上一点到两个焦点距离之和为4;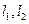 是过点P(0,2)且互相垂直的两条直线,
是过点P(0,2)且互相垂直的两条直线,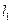 交E于A,B两点,
交E于A,B两点,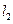 交E交C,D两点,AB,CD的中点分别为M,N。
交E交C,D两点,AB,CD的中点分别为M,N。
(1)求椭圆E的方程;
(2)求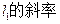 k的取值范围;
k的取值范围;
(3)求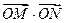 的取值范围。
的取值范围。
已知椭圆E的中心在坐标原点,焦点在x轴上,离心率为
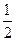 ,且椭圆E上一点到两个焦点距离之和为4;
,且椭圆E上一点到两个焦点距离之和为4;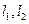 是过点P(0,2)且互相垂直的两条直线,
是过点P(0,2)且互相垂直的两条直线,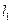 交E于A,B两点,
交E于A,B两点,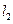 交E交C,D两点,AB,CD的中点分别为M,N。
交E交C,D两点,AB,CD的中点分别为M,N。(1)求椭圆E的方程;
(2)求
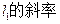 k的取值范围;
k的取值范围;(3)求
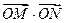 的取值范围。
的取值范围。(1)椭圆方程为
(2)
(3)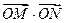 的取值范围是
的取值范围是

(2)

(3)
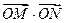 的取值范围是
的取值范围是
解:(1)设椭圆方程为
由
 椭圆方程为
椭圆方程为 …………4分
…………4分
(2)由题意知,直线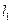 的斜率存在且不为零
的斜率存在且不为零

由 消去
消去 并化简整理,得
并化简整理,得
根据题意,
解得
同理得 …………9分
…………9分
(3)设
那么

同理得
即
 ……10分
……10分


即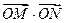 的取值范围是
的取值范围是 …………13分
…………13分

由

 椭圆方程为
椭圆方程为 …………4分
…………4分(2)由题意知,直线
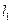 的斜率存在且不为零
的斜率存在且不为零
由
 消去
消去 并化简整理,得
并化简整理,得
根据题意,

解得

同理得
 …………9分
…………9分(3)设

那么


同理得

即

 ……10分
……10分

即
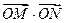 的取值范围是
的取值范围是 …………13分
…………13分
练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
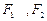 分别是椭圆C:
分别是椭圆C: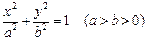 的左右焦点,
的左右焦点,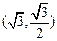 到
到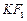 的中点B的轨迹方程。
的中点B的轨迹方程。 )设点P是椭圆C 上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线PM ,PN的斜率都存在,并记为
)设点P是椭圆C 上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线PM ,PN的斜率都存在,并记为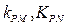 试探究
试探究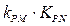 的值是否与点P及直线L有关,并证明你的结论。
的值是否与点P及直线L有关,并证明你的结论。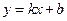 与椭圆
与椭圆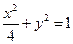 交于
交于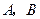 两点,记
两点,记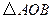 的面积为
的面积为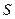 .
.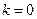 ,
,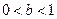 的条件下,
的条件下,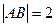 ,
,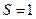 时,求直线
时,求直线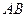 的方程.
的方程.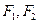 分别是椭圆
分别是椭圆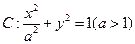 的左右焦点,直线
的左右焦点,直线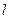 与C相交于A,B两点
与C相交于A,B两点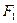 ,若
,若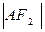 ,
,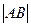 ,
,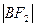 成等差数列,,求
成等差数列,,求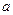 值
值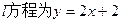 ,且
,且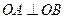 ,求
,求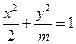 的离心率为
的离心率为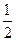 ,则m=" " ( )
,则m=" " ( )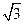 B
B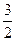 C
C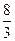 D
D
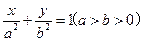 上,AB∥
上,AB∥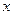 轴,AD过左焦点F,则该椭圆的离心率为 .
轴,AD过左焦点F,则该椭圆的离心率为 .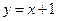 被椭圆
被椭圆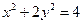 所截得的弦的中点坐标是 ( )
所截得的弦的中点坐标是 ( )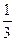 ,
,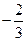 )
)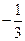 ,
,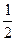 )
)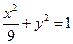 的两个焦点分别为
的两个焦点分别为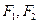 ,点
,点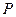 在椭圆上且
在椭圆上且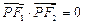 ,则Δ
,则Δ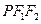 的面积是( )
的面积是( )