题目内容
如图所示,已知A、B、C是长轴长为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且 ,|BC|=2|AC|.
,|BC|=2|AC|.
(1)求椭圆E的方程;
(2)在椭圆E上是否存点Q,使得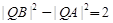 ?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.
?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.
(3)过椭圆E上异于其顶点的任一点P,作 的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明:
的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明: 为定值.
为定值.
(1) ;(2)满足条件的点Q存在,且有两个.
;(2)满足条件的点Q存在,且有两个.
解析试题分析:本题主要考查椭圆的标准方程及其性质,考查学生的转化思想和数形结合思想,考查分析问题解决问题的能力和计算能力.第一问,先由长轴长得到a的值,设出椭圆的标准方程,利用已知条件数形结合得到C点坐标,将C点坐标代入到椭圆中,得到b的值,从而得到椭圆的标准方程;第二问,先设出Q点坐标,利用已知等式计算,可知点Q在直线 上,点
上,点 在直线上,而在椭圆内部,数形结合得存在点Q而且存在2个;法二:用
在直线上,而在椭圆内部,数形结合得存在点Q而且存在2个;法二:用 和椭圆方程联立消参,得到关于x的方程,看方程的判别式,判别式大于0时,方程有2个根,则直线与椭圆有2个交点;第三问,设出点P的坐标,由切线的性质得四点共圆,此圆的圆心为
和椭圆方程联立消参,得到关于x的方程,看方程的判别式,判别式大于0时,方程有2个根,则直线与椭圆有2个交点;第三问,设出点P的坐标,由切线的性质得四点共圆,此圆的圆心为 ,直径为OP,得到此圆的方程,M、N既在此圆上,又在圆O上,2个方程联立,解出直线MN的方程,得出截距的值,再转化出P点坐标代入到椭圆中即可;法二:设出点P、M、N的坐标,利用直线的垂直关系,利用斜率列出等式,转化成直线PM和直线PN的方程,从而得到直线MN的方程.
,直径为OP,得到此圆的方程,M、N既在此圆上,又在圆O上,2个方程联立,解出直线MN的方程,得出截距的值,再转化出P点坐标代入到椭圆中即可;法二:设出点P、M、N的坐标,利用直线的垂直关系,利用斜率列出等式,转化成直线PM和直线PN的方程,从而得到直线MN的方程.
试题解析:(1)依题意知:椭圆的长半轴长 ,则A(2,0),
,则A(2,0),
设椭圆E的方程为 2分
2分
由椭圆的对称性知|OC|=|OB|又∵ ,|BC|=2|AC|
,|BC|=2|AC|
∴AC⊥BC,|OC|=|AC|∴△AOC为等腰直角三角形,
∴点C的坐标为(1,1),点B的坐标为(-1,-1), 4分
将C的坐标(1,1)代入椭圆方程得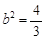
∴所求的椭圆E的方程为 5分
5分
(2)解法一:设在椭圆E上存在点Q,使得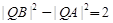 ,设
,设 ,则
,则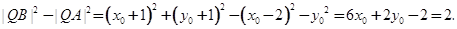
即点Q在直线 上, 7分
上, 7分
∴点Q即直线 与椭圆E的交点,
与椭圆E的交点,
∵直线 过点
过点 ,而点椭圆
,而点椭圆 在椭圆E的内部,
在椭圆E的内部,
∴满足条件的点Q存在,且有两个. 9分
解法二:设在椭圆E上存在点Q,使得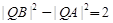 ,设
,设 ,则
,则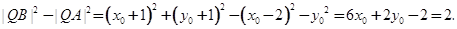
即 , ① -7分
, ① -7分
又∵点Q在椭圆E上,∴ , ②
, ②
由①式得 代入②式并整理得:
代入②式并整理得: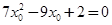 , -③
, -③
∵方程③的根判别式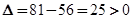 ,
,
∴方程③有两个不相等的实数根,即满足条件的点Q存在,且有两个. 9分
(3)解法一:
设点 ,由M、N是
,由M、N是 的切点知,
的切点知,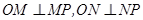 ,
,
∴O、M、P、N四点在同一圆上, 10分
且圆的直径为OP,则圆心为 ,
,
其方程为 , 11分
, 11分
即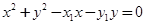 -④
-④
即点M、N满足方程④,又点M、N都在 上,
上,
∴M、N坐标也满足方程 -⑤
-⑤
⑤-④得直线MN的方程为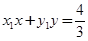 , 12分
, 12分
令 得
得 ,令
,令 得
得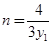 , 13分
, 13分
∴ ,又点P在椭圆E上,
,又点P在椭圆E上,
∴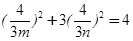 ,即
,即 =定值. 14分
=定值. 14分
解法二:设点 则
则

 名校课堂系列答案
名校课堂系列答案 的方程为
的方程为 ,过原点作斜率为
,过原点作斜率为 的直线和曲线
的直线和曲线 ,过
,过 的直线与曲线
的直线与曲线 ,过
,过 的直线与曲线
的直线与曲线 ,如此下去,一般地,过点
,如此下去,一般地,过点 作斜率为
作斜率为 的直线与曲线
的直线与曲线 ,设点
,设点 (
( ).
). ,并求
,并求 与
与 的关系式(
的关系式( (
( ,向哪一点无限接近?说明理由;
,向哪一点无限接近?说明理由; ,数列
,数列 的前
的前 项和为
项和为 ,试比较
,试比较 与
与 的大小,并证明你的结论.
的大小,并证明你的结论. 轴上的椭圆过点
轴上的椭圆过点 ,且它的离心率
,且它的离心率 .
.
 相切的直线
相切的直线 交椭圆于
交椭圆于 两点,若椭圆上一点
两点,若椭圆上一点 满足
满足 ,求实数
,求实数 的取值范围.
的取值范围. 的离心率为
的离心率为 ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线 相切.
相切. 的标准方程;
的标准方程; 作斜率为
作斜率为 的直线
的直线 交曲线
交曲线 于
于 、
、 两点,且
两点,且 ,又点
,又点 关于原点
关于原点 的对称点为点
的对称点为点 ,试问
,试问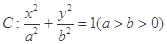 的离心率为
的离心率为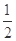 ,以原点
,以原点 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线 相切。
相切。 的标准方程;
的标准方程;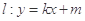 与椭圆
与椭圆 、
、 两点,且
两点,且 ,试判断
,试判断 的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
的面积是否为定值?若为定值,求出定值;若不为定值,说明理由. 与抛物线
与抛物线 的焦点重合,过
的焦点重合,过

 与椭圆相交于不同两点A和B,且满足
与椭圆相交于不同两点A和B,且满足 (O为坐标原点),求实数t的取值范围.
(O为坐标原点),求实数t的取值范围. 的短半轴长为
的短半轴长为 ,动点
,动点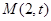
 在直线
在直线 (
( 为半焦距)上.
为半焦距)上. 为直径且被直线
为直径且被直线 截得的弦长为
截得的弦长为 的圆的方程;
的圆的方程;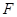 是椭圆的右焦点,过点
是椭圆的右焦点,过点 ,
, 的长为定值,并求出这个定值.
的长为定值,并求出这个定值. 的由顶点为A,右焦点为F,直线
的由顶点为A,右焦点为F,直线 与x轴交于点B且与直线
与x轴交于点B且与直线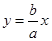 交于点C,点O为坐标原点,
交于点C,点O为坐标原点, ,过点F的直线
,过点F的直线 与椭圆交于不同的两点M,N.
与椭圆交于不同的两点M,N.
 的面积的最大值.
的面积的最大值.  =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N. 时,求k的值.
时,求k的值.