题目内容
如图,椭圆的右焦点 与抛物线
与抛物线 的焦点重合,过
的焦点重合,过 且于x轴垂直的直线与椭圆交于S,T,与抛物线交于C,D两点,且
且于x轴垂直的直线与椭圆交于S,T,与抛物线交于C,D两点,且

(1)求椭圆的标准方程;
(2)设P为椭圆上一点,若过点M(2,0)的直线 与椭圆相交于不同两点A和B,且满足
与椭圆相交于不同两点A和B,且满足 (O为坐标原点),求实数t的取值范围.
(O为坐标原点),求实数t的取值范围.
(1) (2)
(2)
解析试题分析:
(1)抛物线的方程已知,则可以求出右焦点 的坐标为
的坐标为 ,则可以知道
,则可以知道 和直线CD的方程我饿哦x=1,联立直线
和直线CD的方程我饿哦x=1,联立直线 与抛物线方程可以求出C,D两点的坐标,进而得到CD的长度,再联立直线
与抛物线方程可以求出C,D两点的坐标,进而得到CD的长度,再联立直线 与椭圆方程即可求出ST两点的坐标,进而得到ST的距离,利用条件
与椭圆方程即可求出ST两点的坐标,进而得到ST的距离,利用条件 建立关于
建立关于 的等式,与
的等式,与 联立即可求出
联立即可求出 的值,进而得到椭圆的方程.
的值,进而得到椭圆的方程.
(2)因为直线l与椭圆有交点,所以直线l的斜率一定存在,则设出直线l的斜率得到直线l的方程,联立直线l与椭圆方程得到AB两点横纵坐标之间的韦达定理,即 的值,再利用
的值,再利用 发解即可得到P点的坐标,因为P在椭圆上,代入椭圆得到直线斜率k与t的方程,
发解即可得到P点的坐标,因为P在椭圆上,代入椭圆得到直线斜率k与t的方程, ,利用k的范围求解出函数
,利用k的范围求解出函数 的范围即可得到t的范围.
的范围即可得到t的范围.
试题解析:
(1)设椭圆标准方程 ,由题意,抛物线
,由题意,抛物线 的焦点为
的焦点为 ,
, .
.
因为 ,所以
,所以 2分
2分
又
 ,
,
 ,
, ,又
,又

所以椭圆的标准方程 . 5分
. 5分
(2)由题意,直线 的斜率存在,设直线
的斜率存在,设直线 的方程为
的方程为
由 消去
消去 ,得
,得 ,(*)
,(*)
设 ,则
,则 是方程(*)的两根,所以
是方程(*)的两根,所以 即
即 ① 7分
① 7分
且 ,由
,由 ,得
,得
若 ,则
,则 点与原点重合,与题意不符,故
点与原点重合,与题意不符,故 ,
,
所以, 9分
9分
因为点 在椭圆上,所以
在椭圆上,所以 ,即
,即
 ,
,
再由①,得 又
又 ,
, . 13分
. 13分
考点:抛物线椭圆直线与椭圆的位置关系韦达定理

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 的左、右焦点分别
的左、右焦点分别 ,其上顶点为
,其上顶点为 已知
已知 是边长为
是边长为 的正三角形.
的正三角形. 的方程;
的方程; 任作一动直线
任作一动直线 交椭圆
交椭圆 两点,记
两点,记 .若在线段
.若在线段 上取一点
上取一点 ,使得
,使得 ,当直线
,当直线
 的离心率为
的离心率为 ,以原点
,以原点 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线 相切。
相切。 的标准方程;
的标准方程; 与椭圆
与椭圆 、
、 两点,且
两点,且 ,试判断
,试判断 的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
的面积是否为定值?若为定值,求出定值;若不为定值,说明理由. 的离心率
的离心率 ,长轴的左右端点分别为
,长轴的左右端点分别为 ,
, .
. 与曲线
与曲线 ,且与直线
,且与直线 相交于点
相交于点 .问在
.问在 轴上是否存在定点
轴上是否存在定点 ,使得以
,使得以 为直径的圆恒过定点
为直径的圆恒过定点 ,|BC|=2|AC|.
,|BC|=2|AC|.
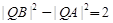 ?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.
?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由. 的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明:
的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明: 为定值.
为定值. ,
, 最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围. 轴对称,它的顶点在坐标原点,点
轴对称,它的顶点在坐标原点,点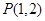 、
、 、
、 均在抛物线上.
均在抛物线上.
 与
与 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求 的值及直线
的值及直线 的斜率.
的斜率. 是椭圆E:
是椭圆E: 的两个焦点,抛物线
的两个焦点,抛物线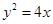 的焦点为椭圆E的一个焦点,直线y=
的焦点为椭圆E的一个焦点,直线y= 上到焦点F1,F2距离之和最小的点P恰好在椭圆E上,
上到焦点F1,F2距离之和最小的点P恰好在椭圆E上,
 的动直线
的动直线 交椭圆于A、B两点,是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由.
交椭圆于A、B两点,是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由.
 =λ
=λ ,直线OP与QA交于点M,问:是否存在点P,使得△PQA和△PAM的面积满足S△PQA=2S△PAM?若存在,求出点P的坐标;若不存在,说明理由.
,直线OP与QA交于点M,问:是否存在点P,使得△PQA和△PAM的面积满足S△PQA=2S△PAM?若存在,求出点P的坐标;若不存在,说明理由.