题目内容
如图2-1-15,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,若AC+BD=a,AC·BD=b,则EF2+EH2=_________.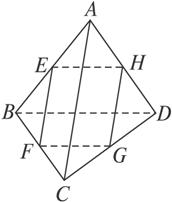
图2-1-15
思路解析:先判断四边形EFGH为何种四边形,研究四条边长与棱AC、BD的关系.
由已知得EF+EH=
(AC+BD)=
,EF·EH=
AC·BD=
,
∴EF2+EH2=(EF+EH)2-2EF·EH=
-
.
答案:
-
练习册系列答案
相关题目
题目内容
如图2-1-15,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,若AC+BD=a,AC·BD=b,则EF2+EH2=_________.
图2-1-15
思路解析:先判断四边形EFGH为何种四边形,研究四条边长与棱AC、BD的关系.
由已知得EF+EH= (AC+BD)=,EF·EH=AC·BD=,
∴EF2+EH2=(EF+EH)2-2EF·EH=-.
答案:-
