Question

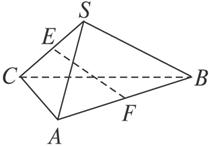
如图2-1-17,空间四边形SABC中,各边及对角线长都相等,若E、F分别为SC、AB的中点,那么异面直线EF与SA所成的角等于(    )

A.90°               B.60°             C.45°           D.30°

         图2-1-17

Answer 1

思路解析:求EF与SA所成的角,可把SA平移,使其角的顶点在EF上,为此取SB的中点G,连结GE、GF、BE、AE.

由三角形中位线定理得GE=BC,GF=SA,且GF∥SA,

所以∠GFE就是EF与SA所成的角.

若设此空间四边形边长为a,那么GF=GE=a,EA=a,

EF=a,因此△EFG为等腰直角三角形,∠EFG=45°,所以EF与SA所成的角为45°.

答案:C