题目内容

2．命题：“?x＞0，x-2≤0”的否定是?x＞0，x-2＞0．

分析 利用特称命题的否定是全称命题写出结果即可．

解答 解：因为特称命题的否定是全称命题，所以命题：“?x＞0，x-2≤0”的否定是：?x＞0，x-2＞0．
故答案为：?x＞0，x-2＞0．

点评 本题考查命题的否定，特称命题与全称命题的否定关系，是基础题．

练习册系列答案
相关题目
12．函数f（x）=$\frac{1}{{{3^x}-1}}$+a（x≠0），则“f（1）=1”是“函数f（x）为奇函数”的（　　）条件．
A．充分不必要B．必要不充分
C．充要D．既非充分又非必要
13．设向量$\overrightarrow{a}$=（2cosx，-2sinx），$\overrightarrow{b}$=$（3cosx，\sqrt{3}cosx）$，f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$．
（1）求函数f（x）的单调增区间和图象的对称中心坐标；
（2）在锐角△ABC中，角A，B，C的对边分别为a，b，c，且f（C）=0，c=1，求a+b的取值范围．
10．已知集合P={x|x2-x≤0}，M={0，1，3，4}，则集合P∩M中元素的个数为（　　）
A．1B．2C．3D．4
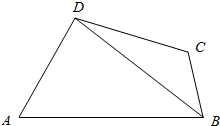17．如图，在四边形ABCD中，AB=8，BC=3，CD=5，∠A=$\frac{π}{3}$，cos∠ADB=$\frac{1}{7}$．
（Ⅰ）求BD的长；
（Ⅱ）求△BCD的面积．
7．已知集合A={（x，y）|x2+（y+1）2≤1}，B={（x，y）|$\sqrt{3}$x+y=4m}，命题p：A∩B=∅，命题q：方程$\frac{{x}^{2}}{2m}$+$\frac{{y}^{2}}{1-m}$=1表示焦点在y轴上的椭圆．
（1）若命题p为真命题，求实数m的取值范围；
（2）若“p∨q”为真，“p∧q”为假，求实数m的取值范围．
14．已知正方体ABCD-A1B1C1D1
（1）求证：平面A1C1D∥平面ACB1：
（2）求证：平面ACB1⊥平面B1BDD1．
11．已知圆台的轴与母线所在直线的夹角为45°，若上底面的半径为1，高为1，求圆台的底面半径．
12．已知f（x）=2asinxcosx+2cos2x，且f（$\frac{π}{6}$）=3．
（1）求实数a的值和最小正周期；
（2）当x∈（-$\frac{π}{4}$，$\frac{π}{4}$），求函数f（x）的值域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网