题目内容
已知数列{an},其中a2=6且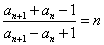 .
.
(1)计算a1,a3,a4;并求数列{an}的通项公式;
(2)设数列{bn}为等差数列,其中bn=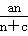
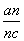 且c为不等于零的常数,求Sn=b1+b2+…+bn
且c为不等于零的常数,求Sn=b1+b2+…+bn
解:(1)∵a2=6, =1,
=1,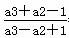 =2,
=2,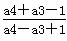 =3,解得a1=1,a3=15,a4=28.
=3,解得a1=1,a3=15,a4=28.
由上面的a1,a2,a3,a4的值可以猜想an=n(2n-1).
下面用数学归纳法加以证明:
①当n=1时,a1=1×(2-1)=1,结论成立.
②假设当n=k时,结论正确,即
ak=k(2k-1),
则当n=k+1时,有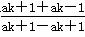 =k,
=k,
∴(k-1)ak+1=(k+1)ak-(k+1)=(k+1)·k(2k-1)-(k+1)=(k+1)(2k2-k-1)
=(k+1)(2k+1)(k-1)(k-1≠0).
∴ak+1=(k+1)[2(k+1)-1].
即当n=k+1时,结论也成立.由①②可知,{an}的通项公式
an=n(2n-1).
(2)∵{bn}是等差数列,∴2b2=b1+b3,即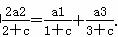
∵a1=1,a2=6,a3=15且c≠0,
由上式解得c=-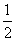 ∴bn=
∴bn=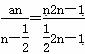 =2n.故Sn=b1+b2+…+bn=n(n+1).
=2n.故Sn=b1+b2+…+bn=n(n+1).

练习册系列答案
相关题目
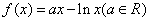 。
。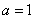 时,求曲线
时,求曲线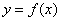 在
在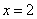 处切线的斜率;
处切线的斜率;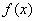 的单调区间;
的单调区间;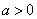 时,求
时,求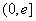 上的最小值。
上的最小值。 的二项展开式中含
的二项展开式中含 的项的系数为
的项的系数为  d B.
d B. d C.
d C. d D.
d D. d
d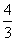 πr3,观察发现V′=S.则四维空间中“超球”的三维测度V=8πr3,猜想其四维测度W=_______.
πr3,观察发现V′=S.则四维空间中“超球”的三维测度V=8πr3,猜想其四维测度W=_______. 则
则 f(x)dx等于 ( ).
f(x)dx等于 ( ). B.
B. C.
C. D.不存在
D.不存在 且
且 ,则
,则 的范围为_____________.
的范围为_____________.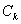 :
: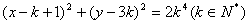 . 下列四个命题:
. 下列四个命题: