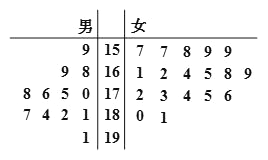
题目内容
【题目】试确定平面上是否存在满足下述条件的两个不相交的无限点集
、
：
（1）在
中，任何三点不共线，且任何两点的距离至少为1；
（2）任何一个顶点在中的三角形，其内部均存在一个中的点，任何一个顶点在中的三角形，其内部均存在一个中的点.
【答案】见解析
【解析】
不存在这样的集合
、
.
用反证法证明.
定义集合中的“凸五点组”为：一个凸多边形，其顶点全部为集合中的点，且其内部和边界上一共恰有集合中的五个点.
因为无限点集中任意两点之间距离至少为1，所以，存在一个边长一定的正方形中至少存在点集中的有限（至少五个）多个点.
设这有限个点的凸包为
边形
.
考虑
内部.
若其内部没有点集中的点，则凸
边形
比原图形少一个点，其内部点一样；若内部有点集中的点，考虑这些点和
、
的凸包为
，则凸多边形
和其内部的点比原图形少一个点（点
）.依次类推，知道得到凸五点组.
在上面这个有限区域中，考虑一个凸五点组
.
1.这个凸五点组的凸包为凸五边形.则在、
、
中均存在点集中的点，分别为
、
、
，故
中有点集中的点
，其在内部，这与为凸五点组矛盾.
2.这个凸五点组的凸包为凸四边形
，内部有点
.则在
、
、
、
中均存在点集中的点，分别为、、、
.若四边形
为凸四边形，则
、
中有点集中的点、
，它们至少有一点不同于.若为中包含，则、中有点集中的点
、
，它们至少有一点不同于.这均与为凸五点组矛盾.
3.这个凸五点组的凸包为，内部有点
、.则在
、、
、
、
中均存在点集中的点，分别为、、、、.若
为凸五边形，则、
、
中有点集中的点、、
，它们互不相同，至少有一点不同于、.若不为凸五边形，则其中一定有一个含于另三点构成的三角形中，不放设中包含点，故、、中有点集中的点、、，它们至少有一点不同于、.这均与为凸五点组矛盾.
综上，这样的无限点集不存在.
练习册系列答案
相关题目
