题目内容
2、下列四个命题：①（a•b）2=a2•b2；②|a+b|＞|a-b|；③|a+b|2=（a+b）2；④若a∥b，则a•b=|a|•|b|．
其中真命题的个数是（ ）
其中真命题的个数是（ ）
分析：逐一对四个命题进行判断，即可得出答案．
解答：解：①（a•b）2=|a|2•|b|2•cos2＜a，b＞≤|a|2•|b|2=a2•b2，故①错误．
②|a+b|与|a-b|大小不确定，故②错误．
③由向量运算性质可得③正确．
④由向量的数量积a•b=|a|•|b|•cos＜a，b＞．当a∥b时，cos＜a，b＞=±1
∴a•b=|a|•|b|或a•b=-|a|•|b|
故③错误．
故选A
②|a+b|与|a-b|大小不确定，故②错误．
③由向量运算性质可得③正确．
④由向量的数量积a•b=|a|•|b|•cos＜a，b＞．当a∥b时，cos＜a，b＞=±1
∴a•b=|a|•|b|或a•b=-|a|•|b|
故③错误．
故选A
点评：本题处理的关键是根据向量的运算性质，逐一判断四个答案中每个答案的真假．
练习册系列答案
相关题目
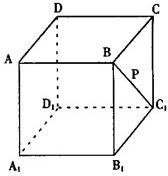15、如图：点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动，则下列四个命题：
如图，正△ABC的中线AF与中位线DE相交于G，已知△A'ED是△AED绕DE旋转过程中的一个图形，现给出下列四个命题：