题目内容
若非负实数x，y满足2x+3y=10，则lgx+lgy的最大值是（ ）A．10
B．25
C．
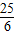
D．lg
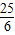
【答案】分析：由题意，正数x，y满足2x+3y=10，由基本不等式可得2x•3y≤（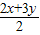
）2=25，故lgx+lgy=lgxy=lg
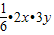≤lg
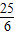，验证等号成立的条件即可．
解答：解：若使对数lgx，lgy有意义，x，y均需为正数，
又x，y满足2x+3y=10，2x•3y≤（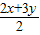
）2=25
故lgx+lgy=lgxy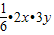=lg
≤lg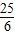
，
当且仅当2x=3y，即x=
，y=
时，取等号．
故lgx+lgy的最大值是lg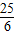
，
故选D
点评：本题考查基本不等式在求解函数最值中的应用，以及对数的运算性质：lgMN=lgM+lgN，属基础题．
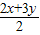）2=25，故lgx+lgy=lgxy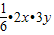=lg≤lg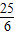，验证等号成立的条件即可．解答：解：若使对数lgx，lgy有意义，x，y均需为正数，
又x，y满足2x+3y=10，2x•3y≤（
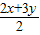）2=25故lgx+lgy=lgxy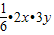=lg
≤lg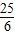，当且仅当2x=3y，即x=
，y=时，取等号．故lgx+lgy的最大值是lg
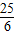，故选D
点评：本题考查基本不等式在求解函数最值中的应用，以及对数的运算性质：lgMN=lgM+lgN，属基础题．
练习册系列答案
相关题目
则z=2x+2y的最大值为 ．