题目内容
设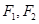 分别为椭圆
分别为椭圆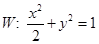 的左、右焦点,斜率为
的左、右焦点,斜率为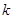 的直线
的直线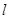 经过右焦点
经过右焦点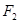 ,且与椭圆W相交于
,且与椭圆W相交于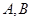 两点.
两点.
(1)求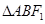 的周长;
的周长;
(2)如果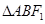 为直角三角形,求直线
为直角三角形,求直线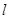 的斜率
的斜率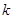 .
.
(1)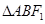 的周长为
的周长为 ;(2)直线
;(2)直线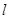 的斜率
的斜率 ,或
,或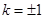 时,
时,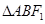 为直角三角形.
为直角三角形.
解析试题分析:(1)求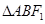 的周长,这是焦点三角问题,解这一类问题,往往与定义有关,本题可由椭圆定义得
的周长,这是焦点三角问题,解这一类问题,往往与定义有关,本题可由椭圆定义得 ,
, ,两式相加即得
,两式相加即得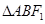 的周长;(2)如果
的周长;(2)如果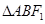 为直角三角形,求直线
为直角三角形,求直线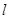 的斜率
的斜率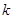 ,由于没教得那一个角为直角,故三种情况,
,由于没教得那一个角为直角,故三种情况, ,或
,或 ,或
,或 ,当
,当 时,此时直线
时,此时直线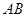 的存在,设出直线方程,代入椭圆方程,设
的存在,设出直线方程,代入椭圆方程,设 ,
, ,由根与系数关系,得到关系式,再由
,由根与系数关系,得到关系式,再由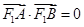 ,即可求出斜率
,即可求出斜率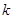 的值,当
的值,当 (与
(与 相同)时,则点A在以线段
相同)时,则点A在以线段 为直径的圆
为直径的圆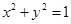 上,也在椭圆W上,求出点
上,也在椭圆W上,求出点 的坐标,从而可得直线
的坐标,从而可得直线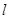 的斜率
的斜率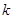 .
.
(1)椭圆 的长半轴长
的长半轴长 ,左焦点
,左焦点 ,右焦点
,右焦点 , 2分
, 2分
由椭圆的定义,得 ,
, ,
,
所以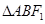 的周长为
的周长为 . 5分
. 5分
(2)因为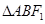 为直角三角形,
为直角三角形,
所以 ,或
,或 ,或
,或 ,再由当
,再由当 时,
时,
设直线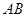 的方程为
的方程为 ,
, ,
, , 6分
, 6分
由  得
得  , 7分
, 7分
所以  ,
,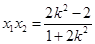 . 8分
. 8分
由 ,得
,得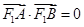 , 9分
, 9分
因为 ,
, ,
,
所以
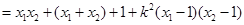
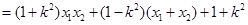
 , 10分
, 10分
解得 .
.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
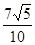 .
.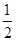 ;
;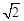 ∶
∶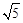 .若能,求P点坐标;若不能,说明理由.
.若能,求P点坐标;若不能,说明理由.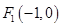 、
、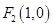 ,动点
,动点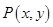 ,且满足
,且满足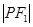 、
、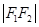 、
、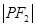
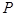 的轨迹
的轨迹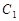 的方程;
的方程;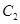 的方程为
的方程为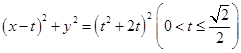 ,过点
,过点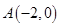 的直线
的直线 与曲线
与曲线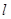 被曲线
被曲线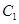 截得的线段长的最小值.
截得的线段长的最小值.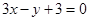 上,若⊿ABC的面积为10,求C点的坐标.
上,若⊿ABC的面积为10,求C点的坐标. (a∈R).
(a∈R).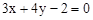 ;
;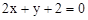 ,它的中心为M
,它的中心为M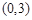 ,求平行四边形另外两条边CB、CD所在的直线方程及平行四边形的面积.
,求平行四边形另外两条边CB、CD所在的直线方程及平行四边形的面积.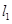 :
: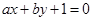 ,(
,( 不同时为0),
不同时为0),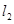 :
: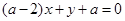 ,
,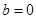 且
且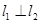 ,求实数
,求实数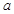 的值;
的值;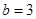 且
且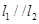 时,求直线
时,求直线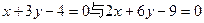 的距离是
的距离是  。
。