题目内容
已知定点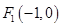 、
、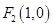 ,动点
,动点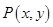 ,且满足
,且满足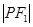 、
、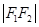 、
、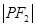
成等差数列.
(1)求点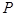 的轨迹
的轨迹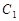 的方程;
的方程;
(2)若曲线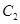 的方程为
的方程为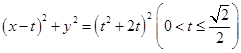 ,过点
,过点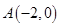 的直线
的直线 与曲线
与曲线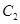 相切,
相切,
求直线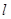 被曲线
被曲线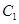 截得的线段长的最小值.
截得的线段长的最小值.
(1)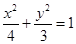 :(2)
:(2)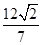 .
.
解析试题分析:(1)利用题中的条件得到椭圆的定义,求出椭圆的实轴长与焦距,然后利用 、
、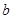 、
、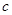 之间的关
之间的关
系求出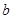 的值,从而确定点
的值,从而确定点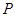 的轨迹
的轨迹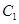 的方程;(2)先设直线
的方程;(2)先设直线 的方程为
的方程为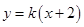 ,利用直线
,利用直线 与圆
与圆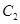
相切,结合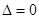 确定
确定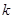 和
和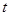 之间的等量关系,然后联立直线与椭圆
之间的等量关系,然后联立直线与椭圆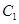 的方程,求出交点的坐标,利用两点
的方程,求出交点的坐标,利用两点
间的距离公式求出弦长的表达式,利用换元法将弦长表达式进行化简,并利用函数单调性求出弦长的最小
值.
(1)由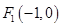 、
、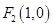 ,
, 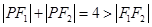 ,
,
根据椭圆定义知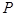 的轨迹为以
的轨迹为以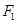 、
、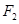 为焦点的椭圆,
为焦点的椭圆,
其长轴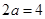 ,焦距
,焦距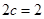 ,短半轴
,短半轴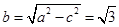 ,故
,故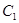 的方程为
的方程为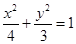 .
.
(2)过点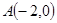 与
与 轴垂直的直线不与圆
轴垂直的直线不与圆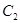 相切,故可设
相切,故可设 :
: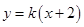 ,
,
由直线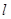 与曲线
与曲线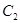 相切得
相切得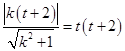 ,化简得
,化简得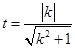 ,
,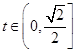 ,
,
由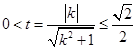 ,解得
,解得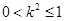 ,
,
联立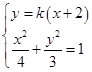 ,消去
,消去 整理得
整理得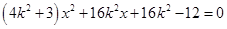 ,
,
直线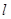 被曲线
被曲线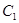 截得的线段一端点为
截得的线段一端点为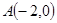 ,设另一端点为
,设另一端点为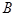 ,
,
解方程可得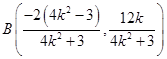 ,
,
有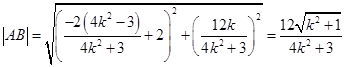 ,
,
令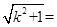 ,则
,则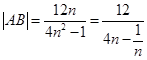 ,
,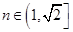 ,
,
考查函数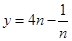 的性质知
的性质知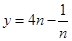 在区间
在区间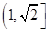 上是增函数,
上是增函数,
所以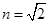 时,
时,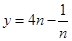 取最大值
取最大值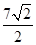 ,从而
,从而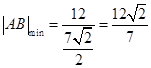 .
.
考点:1.椭圆的定义与方程;2.直线与圆的位置关系;3.直线与椭圆的位置关系;4.两点间的距离

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
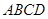 的两条对角线的交点为
的两条对角线的交点为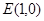 ,且
,且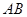 与
与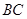 所在的直线方程分别为
所在的直线方程分别为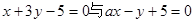 .
.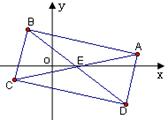
 所在的直线方程;
所在的直线方程;  x上时,求直线AB的方程.
x上时,求直线AB的方程.
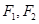 分别为椭圆
分别为椭圆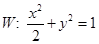 的左、右焦点,斜率为
的左、右焦点,斜率为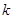 的直线
的直线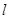 经过右焦点
经过右焦点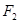 ,且与椭圆W相交于
,且与椭圆W相交于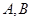 两点.
两点. 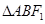 的周长;
的周长; 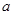 为何值时,直线
为何值时,直线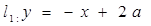 与直线
与直线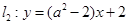 平行?
平行?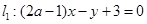 与直线
与直线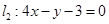 垂直?
垂直? 的顶角
的顶角 的平分线所在直线方程为
的平分线所在直线方程为 ,腰
,腰 的长为
的长为 ,若已知点
,若已知点 ,求腰BC所在直线的方程.
,求腰BC所在直线的方程. 在y轴上的截距为
在y轴上的截距为 ,倾斜角为
,倾斜角为 ,且满足
,且满足 ,则直线
,则直线 的方程为_____________
的方程为_____________ 与
与 垂直,则
垂直,则 ______.
______.