题目内容
已知函数f(x)＝x2－2ax＋b，则“1<a<2”是“f(1)<f(3)”的( )
A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
A解析 函数f(x)＝x2－2ax＋b，所以f(1)＝1－2a＋b，f(3)＝9－6a＋b,1<a<2，所以1－2a<9－6a，即f(1)<f(3)；反过来，f(1)<f(3)时，得1－2a＋b<9－6a＋b得a<2，不能得到1<a<2，所以“1<a<2”是“f(1)<f(3)”的充分不必要条件．
练习册系列答案
作业辅导系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
相关题目
与圆
的位置关系是（ ）
，斜率为1直线
与圆
相交于
、
两点，
为坐标原点， 
，求出直线
，B＝{x|x＋m2≥1}．条件p：x∈A，条件q：x∈B，并且p是q的充分条件，求实数m的取值范围．
，则m的取值范围是( )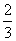
.