题目内容
焦点分别为F1,F2的椭圆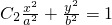 过点M(2,1),抛物线
过点M(2,1),抛物线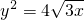 的准线过椭圆C的左焦点.
的准线过椭圆C的左焦点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)不过M的动直线l交椭圆C于A、B两点,若 •
• =0,求证:直线l恒过定点,并求出该定点的坐标.
=0,求证:直线l恒过定点,并求出该定点的坐标.
(Ⅰ)解:由2p= ,∴p=
,∴p= ,∴抛物线
,∴抛物线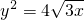 的准线方程为
的准线方程为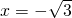 .
.
故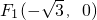 ,
,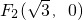 ,
,
∴椭圆方程可化为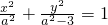 ,又椭圆过点M(2,1),
,又椭圆过点M(2,1),
∴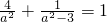 ,则a4-8a2+12=0,
,则a4-8a2+12=0,
∵a2>3,解得:a2=6.
∴所求椭圆的方程为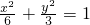 .
.
(Ⅱ)证明:①若直线l⊥x轴,直线l可设为x=m(m≠2),则直线l与椭圆交于
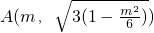 ,
,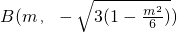 ,
,
由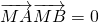 ,得
,得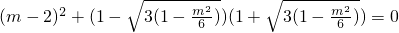 ,
,
即3m2-8m+4=0.
解得:m=2(舍)或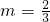 ,
,
故直线l的方程为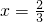 .
.
②若直线l与x轴不垂直,可设直线l的方程为y=kx+n.
直线l与椭圆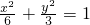 交于A(x1,y1),B(x2,y2).
交于A(x1,y1),B(x2,y2).
由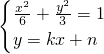 ?(1+2k2)x2+4knx+2n2-6=0.
?(1+2k2)x2+4knx+2n2-6=0.
由△>0,得:(4kn)2-4(1+2k2)(2n2-6)>0,即6k2-n2+3>0.
由根与系数关系得: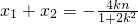 ,
,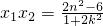 .
.
由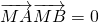 得:(x1-2)(x2-2)+(y1-1)(y2-1)=0,
得:(x1-2)(x2-2)+(y1-1)(y2-1)=0,
即x1x2-2(x1+x2)+y1y2-(y1+y2)+5=0,
又y1=kx1+n,y2=kx2+n,
故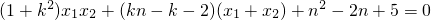 ,
,
即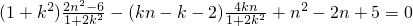 .
.
∴4k2+8kn+(3n+1)(n-1)=0,即(2k+3n+1)(2k+n-1)=0.
∴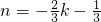 或n=-2k+1.
或n=-2k+1.
而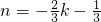 或n=-2k+1满足△>0.
或n=-2k+1满足△>0.
∴直线l为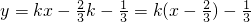 或y=kx-2k+1=k(x-2)+1.
或y=kx-2k+1=k(x-2)+1.
由于直线l不过M,∴直线y=kx-2k+1=k(x-2)+1不合题意.
∴直线l为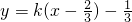 .
.
综合①②,直线l为为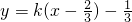 或
或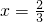 .
.
故直线l恒过定点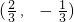 .
.
分析:(Ⅰ)由抛物线方程写出其准线方程,从而求出椭圆焦点坐标,把点M的坐标代入椭圆方程后,结合a2=b2+c2可求椭圆方程;
(Ⅱ)分直线l垂直于坐标轴和不垂直坐标轴两种情况进行讨论,直线垂直坐标轴时,把直线方程代入椭圆方程求出A,B的坐标,由 •
• =0解出m的值,直线不垂直坐标轴时,设出直线方程的斜截式,和椭圆方程联立后由判别式大于0得到直线斜率和在y轴上的截距满足的关系式,再由
=0解出m的值,直线不垂直坐标轴时,设出直线方程的斜截式,和椭圆方程联立后由判别式大于0得到直线斜率和在y轴上的截距满足的关系式,再由 •
• =0把直线的截距用斜率表示,代回直线方程后由线系方程可得直线恒过定点.
=0把直线的截距用斜率表示,代回直线方程后由线系方程可得直线恒过定点.
点评:本题考查了椭圆标准方程的求法,考查了直线和圆锥曲线的位置关系,考查了分类讨论的数学思想,证明直线l恒过定点时,综合考查了向量知识、直线系方程及学生的运算能力,此题属难题.
 ,∴p=
,∴p= ,∴抛物线
,∴抛物线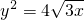 的准线方程为
的准线方程为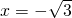 .
.故
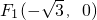 ,
,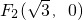 ,
,∴椭圆方程可化为
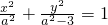 ,又椭圆过点M(2,1),
,又椭圆过点M(2,1),∴
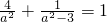 ,则a4-8a2+12=0,
,则a4-8a2+12=0,∵a2>3,解得:a2=6.
∴所求椭圆的方程为
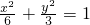 .
.(Ⅱ)证明:①若直线l⊥x轴,直线l可设为x=m(m≠2),则直线l与椭圆交于
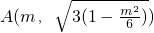 ,
,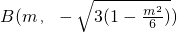 ,
,由
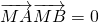 ,得
,得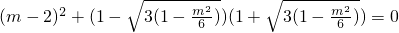 ,
,即3m2-8m+4=0.
解得:m=2(舍)或
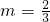 ,
,故直线l的方程为
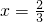 .
.②若直线l与x轴不垂直,可设直线l的方程为y=kx+n.
直线l与椭圆
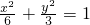 交于A(x1,y1),B(x2,y2).
交于A(x1,y1),B(x2,y2).由
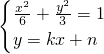 ?(1+2k2)x2+4knx+2n2-6=0.
?(1+2k2)x2+4knx+2n2-6=0.由△>0,得:(4kn)2-4(1+2k2)(2n2-6)>0,即6k2-n2+3>0.
由根与系数关系得:
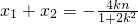 ,
,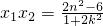 .
.由
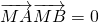 得:(x1-2)(x2-2)+(y1-1)(y2-1)=0,
得:(x1-2)(x2-2)+(y1-1)(y2-1)=0,即x1x2-2(x1+x2)+y1y2-(y1+y2)+5=0,
又y1=kx1+n,y2=kx2+n,
故
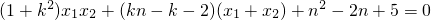 ,
,即
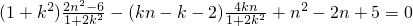 .
.∴4k2+8kn+(3n+1)(n-1)=0,即(2k+3n+1)(2k+n-1)=0.
∴
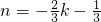 或n=-2k+1.
或n=-2k+1.而
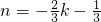 或n=-2k+1满足△>0.
或n=-2k+1满足△>0.∴直线l为
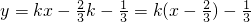 或y=kx-2k+1=k(x-2)+1.
或y=kx-2k+1=k(x-2)+1.由于直线l不过M,∴直线y=kx-2k+1=k(x-2)+1不合题意.
∴直线l为
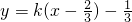 .
.综合①②,直线l为为
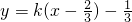 或
或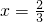 .
.故直线l恒过定点
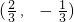 .
.分析:(Ⅰ)由抛物线方程写出其准线方程,从而求出椭圆焦点坐标,把点M的坐标代入椭圆方程后,结合a2=b2+c2可求椭圆方程;
(Ⅱ)分直线l垂直于坐标轴和不垂直坐标轴两种情况进行讨论,直线垂直坐标轴时,把直线方程代入椭圆方程求出A,B的坐标,由
 •
• =0解出m的值,直线不垂直坐标轴时,设出直线方程的斜截式,和椭圆方程联立后由判别式大于0得到直线斜率和在y轴上的截距满足的关系式,再由
=0解出m的值,直线不垂直坐标轴时,设出直线方程的斜截式,和椭圆方程联立后由判别式大于0得到直线斜率和在y轴上的截距满足的关系式,再由 •
• =0把直线的截距用斜率表示,代回直线方程后由线系方程可得直线恒过定点.
=0把直线的截距用斜率表示,代回直线方程后由线系方程可得直线恒过定点.点评:本题考查了椭圆标准方程的求法,考查了直线和圆锥曲线的位置关系,考查了分类讨论的数学思想,证明直线l恒过定点时,综合考查了向量知识、直线系方程及学生的运算能力,此题属难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设圆锥曲线r的两个焦点分别为F1,F2,若曲线r上存在点P满足|PF1|:|F1F2|:|PF2|=4:3:2,则曲线r的离心率等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|