题目内容
在直角坐标系xoy中,曲线C1的参数方程为 (t为参数),P为C1上的动点,Q为线段OP的中点.
(t为参数),P为C1上的动点,Q为线段OP的中点.
(1)求点Q的轨迹C2的方程;
(2)在以O为极点,x轴的正半轴为极轴(两坐标系取相同的长度单位)的极坐标系中,N为曲线p=2sinθ上的动点,M为C2与x轴的交点,求|MN|的最大值.
(1) ;(2)
;(2) .
.
解析试题分析:本题主要考查极坐标方程与直角坐标方程的互化,参数方程与普通方程的互化等数学知识,考查学生的分析问题解决问题的能力、转化能力以及计算能力.第一问,设出Q点坐标,利用中点坐标公式得到P点坐标,而P在 上,代入到
上,代入到 的参数方程中即可得到
的参数方程中即可得到 的参数方程;第二问,利用第一问
的参数方程;第二问,利用第一问 的方程可先求出M点坐标,将曲线
的方程可先求出M点坐标,将曲线 化为直角坐标方程,利用两点间距离公式再利用数形结合即可求出|MN|的最大值.
化为直角坐标方程,利用两点间距离公式再利用数形结合即可求出|MN|的最大值.
试题解析:①设Q(x,y),则点P(2x,2y),又P为C1上的动点,
所以 (t为参数),即
(t为参数),即 (t为参数).
(t为参数).
所以C2的方程为 (t为参数)(或4x+3y-4=0).(4分)
(t为参数)(或4x+3y-4=0).(4分)
②由①可得点M(1,0),且曲线ρ=2sinθ的直角坐标方程为x2+(y-1)2=1,
所以|MN|的最大值为 .(7分)
.(7分)
考点:1.极坐标方程与直角坐标方程的互化;2.参数方程与普通方程的互化.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.已知曲线
轴的非负半轴为极轴建立极坐标系.已知曲线 的极坐标方程为
的极坐标方程为 ,直线
,直线 的参数方程为
的参数方程为 (
( 为参数).
为参数). 在曲线
在曲线 ,以
,以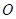 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系,,曲线
轴的非负半轴为极轴建立极坐标系,,曲线 的参数方程为
的参数方程为 .点
.点 是曲线
是曲线 .
. 的值.
的值. .
. 的参数方程为
的参数方程为 (t为参数),直线
(t为参数),直线 ,求|MA|·|MB|.
,求|MA|·|MB|. (φ为参数),曲线C2的参数方程为
(φ为参数),曲线C2的参数方程为 (a>b>0,φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α与C1,C2各有一个交点.当α=0时,这两个交点间的距离为2,当α=
(a>b>0,φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α与C1,C2各有一个交点.当α=0时,这两个交点间的距离为2,当α= 时,这两个交点重合.
时,这两个交点重合. 时,l与C1,C2的交点分别为A1,B1,当α=-
时,l与C1,C2的交点分别为A1,B1,当α=- )=
)= ,曲线P:ρ2-4ρcosθ+3=0,
,曲线P:ρ2-4ρcosθ+3=0, ,直线
,直线 的参数方程为
的参数方程为 (t为参数,
(t为参数, )
)  ,求直线
,求直线 ,半径R=
,半径R= ,求圆C的极坐标方程.
,求圆C的极坐标方程. 中,曲线
中,曲线 的参数方程为
的参数方程为 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点 为极点,
为极点,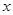 轴的正半轴为极轴的极坐标系下,曲线
轴的正半轴为极轴的极坐标系下,曲线 的方程为
的方程为 .
. 、
、 ,求
,求 .
.