题目内容
给定抛物线C: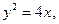 F是C的焦点,过点F的直线
F是C的焦点,过点F的直线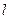 与C相交于A、B两点.
与C相交于A、B两点.
(Ⅰ)设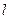 的斜率为1,求
的斜率为1,求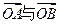 夹角的大小;
夹角的大小;
(Ⅱ)设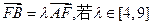 ,求
,求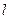 在
在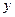 轴上截距的变化范围.
轴上截距的变化范围.
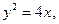 F是C的焦点,过点F的直线
F是C的焦点,过点F的直线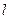 与C相交于A、B两点.
与C相交于A、B两点.(Ⅰ)设
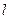 的斜率为1,求
的斜率为1,求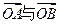 夹角的大小;
夹角的大小;(Ⅱ)设
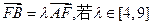 ,求
,求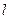 在
在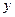 轴上截距的变化范围.
轴上截距的变化范围.(Ⅰ) (Ⅱ)直线l在y轴上截距的变化范围为
(Ⅱ)直线l在y轴上截距的变化范围为
 (Ⅱ)直线l在y轴上截距的变化范围为
(Ⅱ)直线l在y轴上截距的变化范围为
(Ⅰ)C的焦点为F(1,0),直线l的斜率为1,所以l的方程为
将 代入方程
代入方程 ,并整理得
,并整理得 
设 则有
则有 


 所以
所以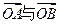 夹角的大小为
夹角的大小为
(Ⅱ)由题设 得
得  即
即
由②得 , ∵
, ∵  ∴
∴ ③
③
联立①、③解得 ,依题意有
,依题意有
∴ 又F(1,0),得直线l方程为
又F(1,0),得直线l方程为

当 时,l在方程y轴上的截距为
时,l在方程y轴上的截距为
由 可知
可知 在[4,9]上是递减的,
在[4,9]上是递减的,
∴
直线l在y轴上截距的变化范围为

将
 代入方程
代入方程 ,并整理得
,并整理得 
设
 则有
则有 


 所以
所以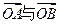 夹角的大小为
夹角的大小为
|
 得
得  即
即
由②得
 , ∵
, ∵  ∴
∴ ③
③联立①、③解得
 ,依题意有
,依题意有
∴
 又F(1,0),得直线l方程为
又F(1,0),得直线l方程为
当
 时,l在方程y轴上的截距为
时,l在方程y轴上的截距为
由
 可知
可知 在[4,9]上是递减的,
在[4,9]上是递减的,∴

直线l在y轴上截距的变化范围为


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
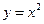 和三个点
和三个点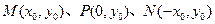
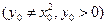 ,过点
,过点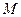 的一条直线交抛物线于
的一条直线交抛物线于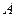 、
、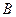 两点,
两点,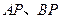 的延长线分别交曲线
的延长线分别交曲线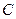 于
于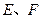 .
.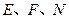 三点共线;
三点共线;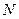 四点共线,问:是否存在
四点共线,问:是否存在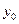 ,使以线段
,使以线段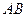 为直径的圆与抛物线有异于
为直径的圆与抛物线有异于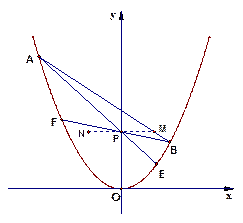
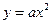 的焦点坐标为
的焦点坐标为 ,则实数
,则实数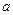 的值为 .
的值为 . =4x的焦点,作直线与此抛物线相交于两点P和Q,那么线段PQ中点的轨迹方程是( )
=4x的焦点,作直线与此抛物线相交于两点P和Q,那么线段PQ中点的轨迹方程是( )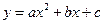 通过点
通过点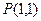 ,且在点
,且在点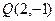 处与直线
处与直线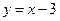 相切,求实数a、b、c的值.
相切,求实数a、b、c的值.