题目内容
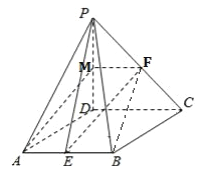
【题目】如图，在四棱锥
中，底面
是棱形， 
， 
平面
， 
，点
、
分别为
和
中点，连接
， 
.
（1）求证：直线
平面
；
（2）求三棱锥
的体积.
【答案】（1）见解析（2）
【解析】试题分析:（1）取
中点
，连接
由三角形中位线定理可得
结合已知可得
，则四边形
为平行四边形，则
，再由线面平行的判定可得直线
（2）连接
，解三角形可得
，再由
，得
，得到
有平面
，过
作
，可得
，求解直角三角形得到
则
到平面
的距离可求，进一步得
到平面
的距离，代入棱锥体积公式可得三棱锥
的体积．
试题解析:（1）证明：作
交
于
，连接
.
∵点
为
中点，∴
.
∵点
为
的中点，∴
.
又
，∴四边形
为平行四边形，∴
，
∴直线
平面
.
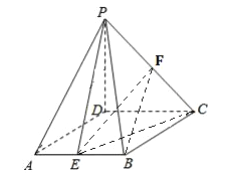
（2）已知
， 
， 
，由余弦定理，得： 
，又
则
设
到面
的距离为
，∵点
为
的中点，∴
，
从而有
.
点睛:本题主要考查,线面间垂直的性质与判定,三棱锥的体积,空间想象能力,推理论证能力.在计算柱,锥,台的体积关键是根据条件找出相应的底面积和高.如果给出的几何体不规则 ,需要利用求体积的一些特殊方法:分割法,补体法,转化法等,它们是解决一些不规则几何体体积计算常用的方法,选择,填空题中使用居多,要熟练掌握.本题使用转化法,将底和高进行转化.
练习册系列答案
相关题目
