题目内容
Pn(xn,yn)是函数y=x2(x≥0)图象上的动点,以Pn为圆心的⊙Pn与x轴都相切,且⊙Pn与⊙Pn+1又彼此外切,若x1=1,xn+1<xn.(1)求证:数列{
| 1 |
| xn |
(2)设⊙Pn的面积为Sn,求证:
| S1 |
| S2 |
| Sn |
3
| ||
| 2 |
分析:(1)由圆Pn与Pn+1相切,且Pn+1与x轴相切可知Rn=Yn,R(n+1)=Y(n+1),且两圆心间的距离就等于两半径之和进而得到
=Yn+Y(n+1),整理得,
-
=2,原式得证.
(2)由(1)可知
=2n-1,进而求得xn的通项公式,代入⊙Pn的面积即可求得的表达式为Sn=(
)4,要证
+
+
+…+
<
,只需证明(x1)2+(x2)2+…(xn)2<
即可.根据1+(
)2+(
)2+…(
)2=
1+(
)2+(
)2+(
)2+…(
)2,且1+(
)2+(
)2+(
)2+…(
)2<2,进而可得1+(
)2+(
)2+…(
)<
,进而得Tn=
+
+
+…+
<
| (xn-xn+1)2+(yn-yn+1)2 |
| 1 |
| xn+1 |
| 1 |
| xn |
(2)由(1)可知
| 1 |
| xn |
| 1 |
| 2n-1 |
| S1 |
| S2 |
| S3 |
| Sn |
3
| ||
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 3 |
| 2 |
| S1 |
| S2 |
| S3 |
| Sn |
3
| ||
| 2 |
解答:解:(1)证:由⊙Pn与x轴都相切,知⊙Pn的半径rn=yn=xn2;又⊙Pn与⊙Pn+1外切,得:|PnPn+1|=rn+rn+1?
=yn+yn+1?(xn-xn+1)2=4ynyn+1=4xn2xn+12.
由xn>xn+1>0得:xn-xn+1=2xnxn+1?
-
=2,
故{
}是首项为1,公差为2的等差数列.
(2)S1=π(x1)4S2=π(x2)4…Sn=π(xn)4
约去
证明(x1)2+(x2)2+…(xn)2<
即可
由(1)知(x1)2+(x2)2+…(xn)2
=1+(
)2+(
)2+…(
)2
因为1+(
)2+(
)2+(
)2+…(
)2
=[1+(
)2+(
)2+…(
)2]+
[1+(
)2+(
)2+(
)2+…(
)2]
即1+(
)2+(
)2+…(
)2=
1+(
)2+(
)2+(
)2+…(
)2
又因为 1+[(
)2+(
)2+(
)2+(
)2+(
)2+(
)2]+(
)2+…
<1+[(
)2+(
)2+(
)2+(
)2+(
)2+(
)2+8(
)2+…
=1+
+
+
…=2
即就是1+(
)2+(
)2+(
)2+…(
)2<2
所以 1+(
)2+(
)2+…(
)<
×2=
即1+(
)2+(
)2+…(
)<
所以
+
+
+…+
<
即 Tn<
| (xn-xn+1)2+(yn-yn+1)2 |
由xn>xn+1>0得:xn-xn+1=2xnxn+1?
| 1 |
| xn+1 |
| 1 |
| xn |
故{
| 1 |
| xn |
(2)S1=π(x1)4S2=π(x2)4…Sn=π(xn)4
约去
| π |
| 3 |
| 2 |
由(1)知(x1)2+(x2)2+…(xn)2
=1+(
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
因为1+(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
=[1+(
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
即1+(
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
又因为 1+[(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 7 |
| 1 |
| 8 |
<1+[(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 8 |
=1+
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
即就是1+(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
所以 1+(
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 3 |
| 4 |
| 3 |
| 2 |
即1+(
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 3 |
| 2 |
所以
| S1 |
| S2 |
| S3 |
| Sn |
3
| ||
| 2 |
即 Tn<
3
| ||
| 2 |
点评:本题主要考查了数列在实际中的应用.本题在数列求和问题时,巧妙的用了分组法,属于难题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 的值;
的值; ,求证:
,求证: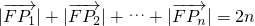 ;
;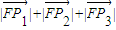 的值;
的值;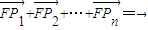 ,求证:
,求证: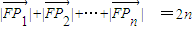 ;
;