��Ŀ����
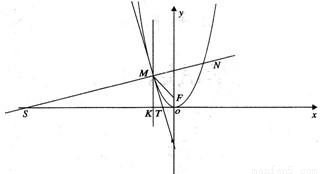
���F��������L��y2=4x�Ľ��㣬P1��x1��y1����P2��x2��y2������Pn��xn��yn����������L�ϵ�n����ͬ�ĵ�n��n��3��n��N*��
��1����������L������P1��P2��P3�ĺ�����֮�͵���4���� ��ֵ��
��ֵ��
��2����n��3ʱ���� ����֤��
����֤��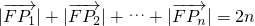 ��
��
��3�����������е������߷���y2=4x�ƹ�Ϊy2=2px��p��0���������С�⣨2����д��һ��һ�㻯�����⼰�������⣬���ж������������٣����������⣬������֤�������Ǽ����⣬��˵�����ɣ�
�⣺��1��������l�Ľ���ΪF��1��0������P1��x1��y1����P2��x2��y2����P3��x3��y3����
�ֱ��P1��P2��P3�������ߵ���l�Ĵ��ߣ�����ֱ�ΪQ1��Q2��Q3��
�� =��x1+
=��x1+ ��+��x2+
��+��x2+ ��+��x3+
��+��x3+ ��=x1+x2+x3+3
��=x1+x2+x3+3
��x1+x2+x3=4���� =7
=7
��2����P1��x1��y1����P2��x2��y2����P3��x3��y3��������Pn��xn��yn�����ֱ��P1��P2��P3������Pn�������ߵ���l�Ĵ��ߣ�����ֱ�ΪQ1��Q2��Q3������Qn
��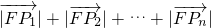 =��x1+1��+��x2+1��+��x3+1��+��+��xn+1��=x1+x2+x3+��+xn+n
=��x1+1��+��x2+1��+��x3+1��+��+��xn+1��=x1+x2+x3+��+xn+n
��
��x1+x2+x3+��+xn=n
��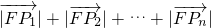 =n+n=2n
=n+n=2n
��3����n��3ʱ���� ����֤��
����֤�� ��
��
�����⣺��n��3ʱ������ ����
���� ��
��
��P1��x1��y1����P2��x2��y2����P3��x3��y3��������Pn��xn��yn�����ֱ��P1��P2��P3������Pn�������ߵ���l�Ĵ��ߣ�����ֱ�ΪQ1��Q2��Q3������Qn
��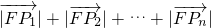 =��x1+
=��x1+ ��+��x2+
��+��x2+ ��+��x3+
��+��x3+ ��+��+��xn+
��+��+��xn+ ��=x1+x2+x3+��+xn+
��=x1+x2+x3+��+xn+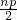
��
��x1+x2+x3+��+xn=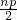
��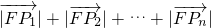 =
=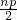 +
+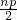 =np
=np
������Ϊ�����⣺ȡn=4ʱ��������l�Ľ���ΪF�� ��0������P1��x1��y1����P2��x2��y2����P3��x3��y3����P4��x4��y4�����ֱ��P1��P2��P3��P4�������ߵ���l�Ĵ��ߣ�����ֱ�ΪQ1��Q2��Q3��Q4��
��0������P1��x1��y1����P2��x2��y2����P3��x3��y3����P4��x4��y4�����ֱ��P1��P2��P3��P4�������ߵ���l�Ĵ��ߣ�����ֱ�ΪQ1��Q2��Q3��Q4��
��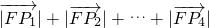 =x1+x2+x3+x4+2p=4p
=x1+x2+x3+x4+2p=4p
��x1+x2+x3+x4=2p
����ȡ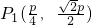 ��
��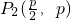 ��
��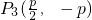 ��
��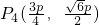 ����
����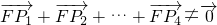
��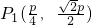 ��
��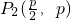 ��
��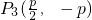 ��
��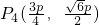 ��һ����n=4ʱ�����������һ��������
��һ����n=4ʱ�����������һ��������
��������1��������l�Ľ���ΪF��1��0������P1��x1��y1����P2��x2��y2����P3��x3��y3�������������ߵĶ��壬���x1+x2+x3=4���ɵý��ۣ�
��2����P1��x1��y1����P2��x2��y2����P3��x3��y3��������Pn��xn��yn�����ֱ��P1��P2��P3������Pn�������ߵ���l�Ĵ��ߣ�����ֱ�ΪQ1��Q2��Q3������Qn�����������ߵĶ���ɵ�x1+x2+x3+��+xn=n���Ӷ���֤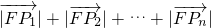 =2n
=2n
��3����n��3ʱ���� ����֤��
����֤�� ��
��
�����⣺��n��3ʱ������ ����
���� ��
��
ȡn=4ʱ��������l�Ľ���ΪF�� ��0������P1��x1��y1����P2��x2��y2����P3��x3��y3����P4��x4��y4�����ֱ��P1��P2��P3��P4�������ߵ���l�Ĵ��ߣ�����ֱ�ΪQ1��Q2��Q3��Q4�����������ߵĶ��壬�ɵ�x1+x2+x3+x4=2p���Ӷ��ɵý��ۣ�
��0������P1��x1��y1����P2��x2��y2����P3��x3��y3����P4��x4��y4�����ֱ��P1��P2��P3��P4�������ߵ���l�Ĵ��ߣ�����ֱ�ΪQ1��Q2��Q3��Q4�����������ߵĶ��壬�ɵ�x1+x2+x3+x4=2p���Ӷ��ɵý��ۣ�
���������⿼�������ߵĶ��壬�������������㣬����Ĺؼ�����ȷ���������ߵĶ��壬�ѶȽϴ�
�ֱ��P1��P2��P3�������ߵ���l�Ĵ��ߣ�����ֱ�ΪQ1��Q2��Q3��
��
 =��x1+
=��x1+ ��+��x2+
��+��x2+ ��+��x3+
��+��x3+ ��=x1+x2+x3+3
��=x1+x2+x3+3��x1+x2+x3=4����
 =7
=7��2����P1��x1��y1����P2��x2��y2����P3��x3��y3��������Pn��xn��yn�����ֱ��P1��P2��P3������Pn�������ߵ���l�Ĵ��ߣ�����ֱ�ΪQ1��Q2��Q3������Qn
��
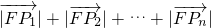 =��x1+1��+��x2+1��+��x3+1��+��+��xn+1��=x1+x2+x3+��+xn+n
=��x1+1��+��x2+1��+��x3+1��+��+��xn+1��=x1+x2+x3+��+xn+n��

��x1+x2+x3+��+xn=n
��
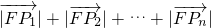 =n+n=2n
=n+n=2n��3����n��3ʱ����
 ����֤��
����֤�� ��
�������⣺��n��3ʱ������
 ����
���� ��
����P1��x1��y1����P2��x2��y2����P3��x3��y3��������Pn��xn��yn�����ֱ��P1��P2��P3������Pn�������ߵ���l�Ĵ��ߣ�����ֱ�ΪQ1��Q2��Q3������Qn
��
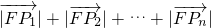 =��x1+
=��x1+ ��+��x2+
��+��x2+ ��+��x3+
��+��x3+ ��+��+��xn+
��+��+��xn+ ��=x1+x2+x3+��+xn+
��=x1+x2+x3+��+xn+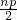
��

��x1+x2+x3+��+xn=
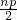
��
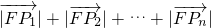 =
=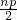 +
+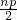 =np
=np������Ϊ�����⣺ȡn=4ʱ��������l�Ľ���ΪF��
 ��0������P1��x1��y1����P2��x2��y2����P3��x3��y3����P4��x4��y4�����ֱ��P1��P2��P3��P4�������ߵ���l�Ĵ��ߣ�����ֱ�ΪQ1��Q2��Q3��Q4��
��0������P1��x1��y1����P2��x2��y2����P3��x3��y3����P4��x4��y4�����ֱ��P1��P2��P3��P4�������ߵ���l�Ĵ��ߣ�����ֱ�ΪQ1��Q2��Q3��Q4����
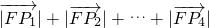 =x1+x2+x3+x4+2p=4p
=x1+x2+x3+x4+2p=4p��x1+x2+x3+x4=2p
����ȡ
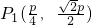 ��
��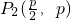 ��
��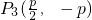 ��
��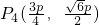 ����
����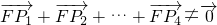
��
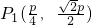 ��
��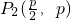 ��
��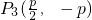 ��
��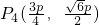 ��һ����n=4ʱ�����������һ��������
��һ����n=4ʱ�����������һ����������������1��������l�Ľ���ΪF��1��0������P1��x1��y1����P2��x2��y2����P3��x3��y3�������������ߵĶ��壬���x1+x2+x3=4���ɵý��ۣ�
��2����P1��x1��y1����P2��x2��y2����P3��x3��y3��������Pn��xn��yn�����ֱ��P1��P2��P3������Pn�������ߵ���l�Ĵ��ߣ�����ֱ�ΪQ1��Q2��Q3������Qn�����������ߵĶ���ɵ�x1+x2+x3+��+xn=n���Ӷ���֤
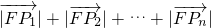 =2n
=2n��3����n��3ʱ����
 ����֤��
����֤�� ��
�������⣺��n��3ʱ������
 ����
���� ��
��ȡn=4ʱ��������l�Ľ���ΪF��
 ��0������P1��x1��y1����P2��x2��y2����P3��x3��y3����P4��x4��y4�����ֱ��P1��P2��P3��P4�������ߵ���l�Ĵ��ߣ�����ֱ�ΪQ1��Q2��Q3��Q4�����������ߵĶ��壬�ɵ�x1+x2+x3+x4=2p���Ӷ��ɵý��ۣ�
��0������P1��x1��y1����P2��x2��y2����P3��x3��y3����P4��x4��y4�����ֱ��P1��P2��P3��P4�������ߵ���l�Ĵ��ߣ�����ֱ�ΪQ1��Q2��Q3��Q4�����������ߵĶ��壬�ɵ�x1+x2+x3+x4=2p���Ӷ��ɵý��ۣ����������⿼�������ߵĶ��壬�������������㣬����Ĺؼ�����ȷ���������ߵĶ��壬�ѶȽϴ�

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ

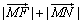 ����СֵΪ4��
����СֵΪ4��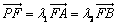 �����жϦ�1+��2�Ƿ�Ϊ��ֵ�����Ƕ�ֵ������ö�ֵ��֤���������Ƕ�ֵ����˵�����ɡ�
�����жϦ�1+��2�Ƿ�Ϊ��ֵ�����Ƕ�ֵ������ö�ֵ��֤���������Ƕ�ֵ����˵�����ɡ�