题目内容
11.若复数z=(m2-m)+mi是纯虚数,则实数m的值为1.分析 根据复数的概念进行求解即可.
解答 解:若复数z=(m2-m)+mi是纯虚数,
则$\left\{\begin{array}{l}{{m}^{2}-m=0}\\{m≠0}\end{array}\right.$,
即$\left\{\begin{array}{l}{m=0或m=1}\\{m≠0}\end{array}\right.$,
即m=1,
故答案为:1
点评 本题主要考查纯虚数的概念,注意虚部不为0,实部为0.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
1.已知复数z=-7-9i,则z的实部和虚部分别为( )
| A. | -7,-9 | B. | -7,-9i | C. | -7,9 | D. | -7,9i |
20.若${C}_{4}^{x}$+${C}_{4}^{x+1}$=5,则x=( )
| A. | 0或3 | B. | 0 | C. | 3 | D. | 2 |
1.A、B、C、D分别是复数z1,z2,z3=z1+z2,z4=z1-z2在复平面内对应的点,O是原点,若|z1|=|z2|,则△COD一定是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
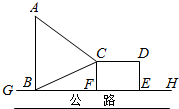 如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建一仓库,并在公路同侧建造一个矩形无顶中转站CDEF(其中边EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,CD=EF+1且∠ABC=60°,设AB=ykm,CF=xkm
如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建一仓库,并在公路同侧建造一个矩形无顶中转站CDEF(其中边EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,CD=EF+1且∠ABC=60°,设AB=ykm,CF=xkm